NCERT Solutions for Science Class 9 Chapter 10
CHAPTER-10 Work and Energy
Intext Exercise 1
Question 1: A force of 7 N acts on an object. The displacement is, say 8 m, in the direction of the force (Fig. 11.3). Let us take it that the force acats on the object through the displacement. What is the work done in this cas?

Answer: In the above question it it given that:
Force is F= 7N
Displacement is S=8 m
Work done is given by the formula:
Work done = Force \(\times\) Displacement
\(W=F\times S=7\times8=56\space Nm\)
Hence, the work done in this case is \(56\space J\).
Intext Exercise 2
Question 1: When do we say tha wordk is done?
Answer: Work is said to be done if the following two conditions are satisfied:
- The force must act on the object.
- The object should be displaced.
Question 2: Write an expression for the work done when a force is acting on an object in the direction of its displacement.
Answer: Consider a cosntant force F acting on an object. It the objec is displaced by a distance \(S\) in the direction of the force (Fig. 11.1) and \(W\) is the work done. Hence, work done is equal to the product of the force and displacement.
Work done = Force \(\times\) Displacement
\(⇒W=F\times S\)
Question 3: Define 1 J of work.
Answer: \(1J\) of work is the amount of work done on an object when a force of \(1N\) displaces it by \(1m\) along the line of action of the force.
Question 4: A pair of bullocks exerts a force of 140 N on a plough. The field being ploughed is 15m long. How much work is done in ploughing the length of the field?
Answer: In the above question it is given that:
Applied force is \(F=140\space N\)
Displacement is \(S=15\space m\)
We know that
Work done = Force \(\times\) Displacement
\(⇒W=F\times S=140\times 15=2100\space J\)
Therefore, work done in ploughing the length of the field is \(2100\space J\).
Intext Exercise 3
Question 1: What is the kinetic energy of an object?
Answer: The enrgy possessed by an object due to its motion is called kinetic energy.
Question 2: Write an experession for the kinetic energy of an object.
Answer: Consider a body of mass ‘m’ to be moving with a velocitt ‘v’. Hence its kinetic energy \(E_k\) is given by:
\(E_k=\frac{1}{2}mv^2\)
The SI unit of kinetic energy is the Joule (J).
Question 3: The kinetic energy of an object of mass, m moving with a velocity of 5 m/s is 25J.What will be its kinetic energy when its velocity is doubled?
What will be its kinetic energy when its velocity is increased three times?
Answer: In the above question it is given that:
Velocity of the objects is 6 m/s.
Kinetic energy of the object is \(E_k=25\space J\)
Mass of the object is \(m\).
We know that,
\(E_k=\frac{1}{2}mv^2\)
Case 1: When tha velocity of an object is doubled.
\(v=10\space m/s\)
Kinetic Energy is given by:
\(E_k=\frac{1}{2}mv^2\)
\(E_k∝v^2\)
Hence, when \(v=10\space m/s\)
\(E_k=25\times4=100\space J\)
The kinetic energy becomes 4 times its initial value.
Case 2: If velocity is increased three times, then its kinetic energy will be nine times its original value, as \(E_k∝v^2\).
Hence, kinetic energy will be:
\(E_k=25\times9=225\space J\)
Thus, Kinetic energy becomes nine times its initial value.
Intext Exercise 4:
Question 1: Whas is power?
Asnwer: Power is defined as the rate of doing work or the rate of transfer of energy. If \(W\) is the amount of work done in time \(t\), then power is given by:
\(Power=\frac{Work\space done}{Time}=\frac{Energy}{Time}\)
\(P=\frac{W}{T}\)
The S.I. unit power is watt (W).
Question 2: Define 1 watt of power.
Answer: The power of an agent, which does work at the rate of 1 joule pers second is defined as 1 watt. It is also said that power is 1 W when the rate of consumption of energy is 1 J/s.
\(1W=\frac{1J}{1s}\)
Question 3: A lamp consumes 1000 J of electrical energy in 10 s. What is its power?
Answer: In the above qustion it is given that:
Energy consumed is \(E=10000\space J\)
Time \(T=10\space s\)
\(Power=\frac{Work\space done}{Time}=\frac{Energy}{Time}\)
\(⇒Power=\frac{1000}{10}=100W\)
Question 4: Define average power:
Answer: Average power is defined as the power obtained by dividing the total amount of work done in the total time taken to do this work.
Average power \(=\frac{Total\space work\space done}{total\space time\space taken}\)
NCERT Exercise:
Question 1: Look at the activities listed below. Reason out whether or not work is done in the light of your understanding of the term ‘work’.
● Suma is swimming in a pond.
● A donkey is carrying a load on its back.
● A wind mill is lifting water from a well.
● A green plant is carrying out photosynthesis.
● An engine is pulling a train.
● Food grains are getting dried in the sun.
● A sailboat is moving due to wind energy.
Answer: According to the definition, work is done whenever the following two conditions are satisfied:
1. A force acts on the body.
2. There is a displacement of the body by the application of force in or opposite to the direction of force.
Therefore,
● In this case of swimming, Suma applies a force to push the water backwards. This allows Suma to swim in the forward direction by the forward response of water. Hence, the force causes a displacement.
Thus, while swimming work is done by Suma.
● In this case the donkey applies a force in the upward direction while carrying a load. But the displacement of the load is in the forward direction. As the displacement is perpendicular to force, the work done is zero.
● In this case work is done by the windmill in lifting water from the well as a windmill works against the gravitational force to lift water.
● In this case there is no displacement of the leaves of the plant. Hence, the work done is zero.
● In this case an engine applies force to pull the train. This makes the train move in the direction of the applied force. Thus, there is a displacement in the train in the same direction. Hence the work is done by the engine on the train.
● In this case during the process of food grains getting dried in the sun, no work is done as food grains do not displace in the presence of solar energy.
● In this case wind energy applies a force on the sailboat to push it in a forward direction. Therefore, the displacement of the boat is along the direction of the force. Hence, the work is done by wind on the boat.
Question 2: An object thrown at a certain angle to the ground moves in a curved path and falls back to the ground. The initial and the final points of the path of the object lie on the same horizontal line. What is the work done by the force of gravity on the object?
Ans: In the above question the object thrown at a certain angle to the ground moves in a curved path and falls back to the ground. The initial and the final points of the path of the object lie on the same horizontal line.
Work done by the force of gravity on an object depends only on vertical displacement. Vertical displacement is given by the difference in the initial and final positions (height) of the bject, which is zero.
Work done by gravity is expressed as, W =mgh
Where,
m is the mass of the object,
g is the acceleration due to gravity
h is the vertical displacement, which is zero.
\(⇒W=mg(0)=0J\)
Thus, the work done by gravity on the given object is zero joules.
Question 3: battery lights a bulb. Describe the energy changes involved in the process.
Answer: Once a bulb is connected to a battery its chemical energy is converted into electrical energy. When the bulb receives this electrical energy, it is converted into light and heat energy. Therefore, the transformation of energy in the given situation can be shown as:
Chemical Energy → Electrical Energy → Light Energy →Heat Energy
Question 4: Certain force acting on a 20 kg mass changes its velocity from 5m/ s to 2m/ s . Calculate the work done by the force.
Answer: Change in kinetic energy is defined as the work done.
It is given that a 20 kg mass changes its velocity from 5m/ s to 2m/ s .
Kinetic energy is given by the expression,
\((E_k)v=\frac{1}{2}mv^2\)
Where,
\(E_k\)= Kinetic energy of the object moving with a velocity, \(v\)
\(m\)= Mass of the object
Kinetic energy when the object was moving with a velocity 2m/s,
\((E_k)_2=\frac{1}{2}\times20\tomes(2)^2=40J\)
Therefore, work done by force \(=40-250=-210J\)
Here, the negative sign shows that the force is acting in the opposite direction of the motion of the object.
Question 5: A mass of 10 kg is at point A on a table. It is moved to point B. If the line joining A and B is horizontal, what is the work done on the object by
the gravitational force? Explain your answer.
Answer: Work done by gravity depends only on the vertical displacement of the body. It does not depend upon the path of the body. Hence, work done by gravity is given by:
W=mgh
Where,
Vertical displacement, h=0
\(⇒W=mg(0)=0J\)
Thus, the work done by gravity on the object is zero joules.
Question 6: The potential energy of a freely falling object decreases progressively. Does this violate the law of conservation of energy? Why?
Answer: When the body drops from a height, its potential energy changes into kinetic energy progressively. A decrease in the potential energy is equivalent
to an increase in the kinetic energy of the body.
During this process, the total mechanical energy of the body is conserved.
Therefore, the law of conservation of energy is not violated.
Question 7: What are the various energy transformations that occur when you are riding a bicycle?
Answer: When we ride a bicycle, our muscular energy is transferred into the bicycle’s heat energy and kinetic energy. Heat energy heats the body and kinetic energy provides a velocity to the bicycle. The transformation can be shown as:Muscular Energy Kinetic → Energy→Heat energy
The total energy is conserved in the entire transformation of energies.
Question 8: Does the transfer of energy take place when you push a huge rock with all your might and fail to move it? Where is the energy you spend going?
Answer: When we push a huge rock there is no transfer of energy because there is no transfer of muscular energy to the stationary rock. Instead muscular energy is transferred into heat energy, which causes our body to become hot.
Question 9: A certain household has consumed 250 units of energy during a month. How much energy is this in joules?
Answer: We know tha 1 unit of energy is equal to 1 kilowatt hour (kWh).
1 unit = 1kWh
Therefore,
\(1kWh=3.6\times10^6J\)
Hence, 250 unit of energy \(=250\times3.6\times10^6=9\times10^8J\)
Questuin 10: An object of mass 40 kg is raised to a height of 5 m above the ground. What is its potential energy? If the object is allowed to fall, find its kinetic energy when it is half-way down.
Answer: In the above question it is given that:
h = Vertical displacement = 5 m
m = Mass of the object = 40 kg
g = Acceleration due to gravity \(=9.8\space m/s^2\)
Gravitational potential energy is given by the expression,
W = mgh
\(⇒W=40\times5\times9.8=1960J\)
At half-way down, the potential energy of the object will reduce to half i.e.,
\(\frac{1960}{2}=980J\)
At this point, the object has potential energy equal to kinetic energy. This is due to the law of conservation of energy. Hence, half-way down, the kinetic energy of the object will be 980J .
Question 11: What is the work done by the force of gravity on a satellite moving round the earth? Justify your answer.
Answer: When the direction of force is perpendicular to displacement, the work done is zero. If a satellite moves around the Earth the direction of force of gravity on the satellite is perpendicular to its displacement. Therefore, the work done on the satellite by the Earth is zero.
Question 12: Can there be displacement of an object in the absence of any force acting on it? Think. Discuss this question with your friends and teacher.
Answer: Yes, there can be displacement of an object in the absence of any force acting on it by moving with uniform velocity. Suppose an object is moving with constant velocity, then the net force acting on it is zero. Hence, there can be a displacement without a force.
Question 13: A person holds a bundle of hay over his head for 30 minutes and gets tired. Has he done some work or not? Justify your answer.
Answer: If a person holds a bundle of hay over his head gravitational force is acting on the hay downwards. But, there is no displacement in the bundle of hay in the direction of force. Hence, no work is done.
Question 14: An electric heater is rated 1500 W. How much energy does it use in 10 hours?
Answer: Energy consumed by an electric heater is given by the expression,
\(P=\frac{W}{T}\)
Where,
\(P=1500\spaceW=1.5\spacekW\)
\(T=10\space hrs\)
Work done = Energy consumed by the heater
Hence, energy consumed \(=Power\times Time=1.5\times10=15kWh=1.5\times10=15\space kWh\).
Question 15: Illustrate the law of conservation of energy by discussing the energy changes which occur when we draw a pendulum bob to one side and
allow it to oscillate. Why does the bob eventually come to rest? What happens to its energy eventually? Is it a violation of the law of conservation of energy?
Answer: According to the “law of conservation of energy”: Energy can be neither created nor destroyed. It can only be converted from one form to another. Consider the case of an oscillating pendulum.

When a pendulum moves from its mean position P to either of its extreme positions A or B, it rises through a height h above the mean level P. At the extreme point, bob comes to rest and the kinetic energy of the bob is transformed into potential energy.
As it moves towards point P, its potential energy decreases progressively.
Simultaneously, the kinetic energy increases.
As the bob reaches point P, its potential energy is converted to kinetic energy.
At this point bob possesses only kinetic energy. This process is repeated as
long as the pendulum oscillates. The bob does not oscillate forever. It comes to rest due to some friction in the air.
The pendulum loses energy overcoming this friction. After all the energy is lost, it comes to rest. The law of conservation of energy holds here as the energy lost by the pendulum to overcome friction is gained by its surroundings. Hence, the total energy of the pendulum and the surrounding system is conserved.
Question 16: An object of mass, m is moving with a constant velocity, v. How much work should be done on the object in order to bring the object to rest?
Answer: When a body is in motion it possesses kinetic energy. Kinetic energy of an object of mass, m moving with a velocity, v is given by the expression,
\(E_k=\frac{1}{2}mv^2\)
Therefore, \(\frac{1}{2}mv^2\) amount of work is required to be done on the object to bring the object to rest.
Question 17: Calculate the work required to be done to stop a car of 1500 kg moving at a velocity of 60 km/h?
Answer: In the above question it is given that:
Mass of car, m = 1500 kg
Velocity of car, \(v=60\space km/h=60\times\frac{5}{18}m/s\)
Kinetic energy is given by:
\(E_k=\frac{1}{2}mv^2\)
\(⇒E_k=\frac{1}{2}(1500)(60\times\frac{5}{18})^2=20.8\times10^4J\)
Hence, \(20.8\times10^4J\) needs to be done to stop the car.
Question 18: In each of the following, a force F is acting on an object of mass, m. The direction of displacement is from west to east shown by the longer
arrow. Observe the diagrams carefully and state whether the work done by the force is negative, positive or zero.
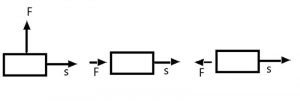
Answer: Following cases are explained below:
Case I
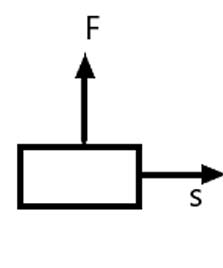
Here the direction of force acting on the block is perpendicular to the displacement.
Hence, work done by force on the block will be zero.
Case II
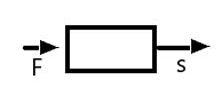
Here the direction of force acting on the block is in the direction of displacement. So, work done by force on the block will be positive.
Case III
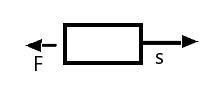
Here the direction of force acting on the block is opposite to the direction of displacement. Hence, work done by force on the block will be negative.
Question 19: Soni says that the acceleration in an object could be zero even when several forces are acting on it. Do you agree with her? Why?
Answer: Acceleration of an object will be zero when the net force acting on an object will be zero. Net force can be zero even when there are multiple forces acting on the body. For a uniformly moving object, the net force acting on the object is zero. Hence, the acceleration of the object is zero. Hence, Soni is right.
Question 20: Find the energy in kWh consumed in 10 hours by four devices of power 500 W each.
Answer: In the abow question it is given that:
P=500 W=0.5 kW
T = 10 hrs
Energy consumed by an electric device can be obtained with the help of the expression given below:
\(P=\frac{W}{T}\)
Where
Work done = Energy consumed by the device
Energy consumed by each device = Power \(\times\) Time
Work done \(=0.5\times10=5\space kWh\)
Hence, the energy consumed by four equal rting devices in 10 hrs will be \(4\times5\space kWh=20\space kWh\)
Question 21: A freely falling object eventually stops on reaching the ground. What happens to its kinetic energy?
Answer: Once the object hits the hard ground, the kinetic energy gets converted into heat energy and sound energy. Further, entire energy is lost to the environment. This energy can also deform the ground with respect to the nature of the ground and the amount of kinetic energy possessed by the object.
Study materials
- Refernce Books
- NCERT Solutions
- Syllabus








