NCERT Solutions for Maths Class 9 Chapter 8

CHAPTER 8

Exercise 8.1:

Question 1: If the diagonals of a parallelogram are equal, then show that it is a rectangle.

Answer: Given that the diagonals of aparallelogram are equal. Let us assume a parallelogram \(ABCD\) whose diagonals are equal as shown in the figure below.

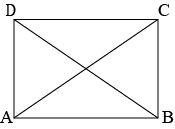
Here \(ABCD\) is a parallelogram, so we can write that \(AB=DC\) since opposite sides of a parallelogram are equal.

Consider the triangle \(ABC\) and \(DCB\). In these two triangles we have \(AB=DC,\space BC=BC\) and as per given data \(AC=DB\). So, we can write that \(\triangle ABC≅\triangle DCB\) by SSS Congruence rule.

\(⇒\angle ABC=\angle DCB\)

Wo know that the sum of the angles on the same side of the trasversal is \(180^0\).

\(∴\angle ABC+\angle DCB=180^0\)

Substitute the value \(\angle ABC=\angle DCB\) in the above equation.

\(⇒\angle ABC+\angle ABC=180^0\)

\(⇒2\angle ABC=180^0\)

\(⇒\angle ABC=\frac{180^0}{2}\)

\(⇒\angle ABC=90^0\)

Here we have the angle \(ABC\) and \(DCB\) as \(90^0\). When the angles of the parallelogram are equal to \(90^0\), then it is called as Rectangle.

Hence, if the digonals of the parallelogram equal then it is called Rectangle.

Question 2: Show that the diagonals of a square are equal and bisect other at right angles.

Answer: Consider a square \(ABCD\) whose diagonals are \(AC\) and \(BD\). The intersecting point of the diagonals will be \(O\) as show in below figure.

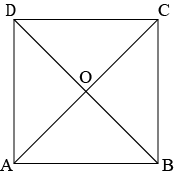
According to the given statement we need to prove that \(AC=BD,\space OA=OC,\space OB=OD\) and \(\angle AOB=90^0\)

Consider \(\triangle ABC\) and \(\triangle DCB\).

\(AB=DC\) since the sides of square are equal, \(\angle ABC=\angle DCB=90^0\) and \(BC=CB\).

So, by using SAS congruency law we can say that \(\triangle ABC≅\triangle DCB\).

\(∴AC=DB\) by \(CPCT\).

Hence, the diagonals of the square aew equal in length.

Now consider \(\triangle AOB\) and \(\triangle COD\)

In both the triangles we can write.

\(\angle AOB=\angle COD\) sicnce vertically opposite angles are equal,

\(\angle ABO=\angle CDO\) since alternate interior angles are also equal and

\(AB=CD\) since the sides of square are always equal.

So, by using AAS congruence rule we can say that \(\triangle AOB≅\triangle COD\).

\(∴AO=CO\) and \(OB=OD\) by \(CPCT\)

Now consider \(\triangle AOB\) and \(\triangle COB\),

As we have proved earlier \(AO=CO\),

\(AB=CB\) since sides of a square are equal.

\(BO=BO\)

By using SSS congruency rule we can write thaht \(\triangle AOB≅\triangle COB\).

\(∴\angle AOB=\angle COB\) by CPCT

But the angles \(AOB\) and \(COB\) are linear pair.

\(∴\angle AOB+\angle COB=180^0\)

\(2\angle AOB=180^0\)

\(\angle AOB=90^0\)

Hence, the diagonals of a square busect other at right angles.

Question 3: Diagonals \(AC\) of parallelogram \(ABCD\) bisects \(\angle A\) as shown in figure.

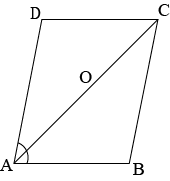
(i) Show that it bisects \(\angle C\)

Answer: Give that \(ABCD\) is a parallelogram

\(∴\angle DAC=\angle BCA\) and \(\angle BAC=\angle DCA\) since alternative interior angles

But in the problem, we have given that \(AC\) bisect \(\angle A\)

\(\angle DAC=\angle BCA=\angle BAC=\angle DCA\)

\(\angle DCA=\angle BAC\)

Hence, \(\angle AC\) bisects \(\angle C\)

(ii) Show that \(ABCD\) is a rhombus

Answer: From the equation \(\angle DAC=\angle BCA=\angle BAC=\angle DCA\), we can writethat \(\angle DAC=\angle DCA\).

\(DA=DC\) since side opposite to equal angles are equal.

But we have \(DA=BC\) and \(AB=CD\) since opposite sides of the parallelogram are equal.

\(AB=BC=CD=DA\)

Question 4: \(ABCD\) is a rectangle in which diagonal \(AC\) bisects \(\angle A\) as well as\(\angle C\).

(i) Show that \(ABCD\) is a square.

Answer: It is given that \(ABCD\) is a rectangle. So, we can write that

\(\angle A=\angle C\)

\(⇒\frac{1}{2}\angle A=\frac{1}{2}\angle C\)

But they have mentioned that \(AC\) bisects \(\angle A\) as well as \(\angle C\)

\(⇒\angle DAC=\frac{1}{2}\angle DCA\)

\(∴CD=DA\) since sides opposite to equal angles are also equal.

But \(DA=BC\) and \(AB=CD\) since opposite sides of rectangle are equal.

\(∴AB=BC=CD=DA\)

Here \(ABCD\) is given to be a rectagnle, but all the sides are equal.

Hence \(ABCD\) is a square

(ii) Show that diagonal \(BD\) bisects \(\angle B\) as well as \(\angle D\)

Answer: Now consider \(\triangle BCD\), in this triangle we can write that 

\(BC=CD\) since sides of a square are equal.

\(\angle CDB=\angle CBD\) since angles opposite to equal sides are equal.

But we have \(\angle CDB=\angle ADB\) since altrenate interior angles for parallel lines \(AB\) and \(CD\).

\(∴\angle CBD=\angle ABD\)

Hence \(BD\) bisects \(\angle B\)

Also, \(\angle CBD=\angle ADB\) which are alternate interior angles for parallel lines \(BC\) and \(AD\).

\(∴\angle CDB=\angle ADB\)

Finally, \(BD\) bisects \(\angle D\) and \(\angle B\).

Question 5: In parallelogram (ABCD\), two points \(P\) and \(Q\) are taken on diagonal \(BD\) such that \(DP=BQ\) as shown in below figure.

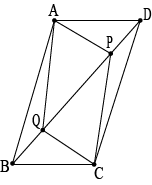
(i) show that \(\triangle APD≅\triangle CQB\)

Answer: Consider \(\triangle APD\) and \(\triangle CQB\), in these two triangles we can write

\(\angle ADP=\angle CBQ\) since alternate interior angles for the parallel lines \(BC\) and \(AD\),

\(AD=CB\) since ipposite sides of parallelogram are equal

\(DP=BQ\) which is in the given data.

By using SAS congruence rule, we can say that \(\triangle APD≅\triangle CQB\)

(ii) Show that \(AP=CQ\)

Answer: As we have \(\triangle AQB\) and \(\triangle CPD\), in these two triangles we can write

\(\angle ABQ≅\angle DCP\) since leternate interior angles for the parallel lines \(AB\) and \(CD\),

\(AB=CD\) since opposite sides of parallelogram are equal.

\(BQ=DP\) which is in the given data.

By using SAS congruence rule, we can say that \(\triangle AQB≅\triangle CPD\)

(iv) Show tha \(AQ=CP\)

Answer: As we have \triangle AQB≅\triangle CPD\). By using CPCT we can write that \(AQ=CP\).

(v) Show that APCQ is a Parallelogram

Answer: From the result obtaines from (ii) and (iv) which are \(AQ=CP\) and \(AP=CQ\). That means the opposite sides of the quadrilateral \(APCQ\) are equal, so \(APCQ\) is a parallelogram.

Question 6: \(ABCD\) is a parallelogram and \(AP\) and \(CQ\) perpendiculars from vertices \(A\) and \(C\) on diagonal \(BD\) as shown figure.

(i) Sshow that \(\triangle APB≅\triangle CQD\)

Answer: Consider \(\triangle APB\) and \(\triangle CQD\), in these two triangles awe can write that 

\(\angle APB=\angle CQD=90^0\)

\(AB=CD\) since opposite sides of parallelogram,

\(\angle ABP=\angle CDQ\) since alternate interior angles for parallel lines \(AB\) and \(CD\).

By using AAS congruency rule we can say that \(\triangle APB≅\triangle CQD\)

(ii) Show that \(AP=CQ\)

Answer: From the statement \(\triangle APB≅\triangle CQD\), by using CPCT we can write that \(AP=CQ\).

Question \(ABCD\) is a trapezium on which \(AB\parallel CD\) and \(AD=BC\) as show in figure. (Hint: Extend \(AB\) and draw a line through \(C\) parallel to \(DA\) intersecting \(AB\) at point \(E\).

(i) Show that \(\angle A=\angle B\)

Answer: We have \(AD=CE\) opposite sides of parallelogram and \(AD=BC\).

\(∴BC=CE\) and \(\angle CEB=\angle CBE\) since angle opposite to equal sides are also equal.

Consider the parallel lines \(AD\) and \CE\). \(AE\) is the transversal line for them.

So,

\(\angle A+\angle CEB=90^0\) sicne angles on the same sides of transversal.

\(⇒\angle A+\angle CBE=180^0\)

Also, \(\angle B+\angle CBE=180^0\) as they are linear pair of angles. So, from these two equals we can write that

\(\angle A=\angle B\)

(ii) Show that \(\angle C=\angle D\)

Answer: Given \(AB\parallel CD\), so

\(\angle A+\angle D=180^0\), \(\angle C+\angle B=180^0\) since angles on the same side of the transversal.

\(∴\angle A+\angle D=\angle C+\angle B\)

But we have \(\angle A=\angle B\), so we will have

\(\angle C=\angle D\)

(iii) Show that \(\triangle ABC≅\triangle BAD\)

Answer: Consider \(\triangle ABC\) and \(\triangle BAD\), in these two triangles we can write that

\(AB=BA,\space BC=AD\) and \(\angle B=\angle A\)

By using SAS congruence rule, we can say that \(\triangle ABC≅\triangle BAD\).

(iv) Show that diagonal \(AC=\) diagonal \(BD\)

Answer: We have \(\triangle ABC≅\triangle BAD\), so by usning CPCT we can write that \(AC=BD\)

Exercise 8.2:

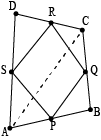
Question: \(ABCD\) is a quadrilateral in which \(P,\space Q,\space R\) and \(S\) are mid-points of the sides \(AB,\space BC,\space CD\) and \(DA\) (se the given figure). \(AC\) is diagonal. show that:

(i) \(SR\prarallel AC\) and (SR=\frac{1}{2}AC\)

(ii) \(PQ=SR\)

(iii) \(PQRS\) is parallelogram.

Answer: 

Given: \(ABCD\) is quadrilateral

Tor prove: 

(i) \(SR\parallel AC\) and \(SR=\frac{1}{2}AC\)

(ii) \(PQ=SR\)

(iii) \(PQRS\) is aparallelogram

(i) \(\triangle ADC\), \(S\) and \(R\) are the mid-points of sides \(AD\) and \(CD\) respectively.

In a triangle, the line segment connecting the midpoints of any two sides is parallel to and half of the third side.

\(∴SR\parallel AC\) and \(SR=\frac{1}{2}AC\)  …(1)

(ii) In \(\triangle ABC,\space P\) and \(Q\) are mid-point of sides \(AB\) and \(BC\) respectively. Therefore, by using midpoint theorem,

\(PQ\parallel AC\) and \(PQ=\frac{1}{2}AC\) …. (2)

Using Equation (1) and (2), we obtain

\(PQ\parallel SR\) and \(PQ=\frac{1}{2} SR\)  ..(3)

\(∴Pq=SR\)

(iii) From Equation (3), we obtained

\(PQ\parallel SR\) and \(PQ=SR\)

Clearly, one pair of quadrilateral \(PQRS\) opposing sides is parallel and equal. \(PQRS\) is thus a parallelogram.

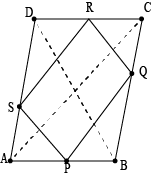
Question 2: \(ABCD\) is rhombus and \(P,\space Q,\space R\) and \(S\) are the mid-points of the sides \(AB,\space BC,\space CD\) and \(DA\) respectively. Show that the quadrilateral \(PQRS\) is a rectangle.

Answer: 

Given: \(ABCD\) is a rhombus and \(P,\space Q,\space R\) and \(S\) are the mid-points of the sides \(AB,\space BC,\space CD\) and \(DA\) respectively.

To find: Quadrilateral \(PQRS\) is a rectangle.

In \(\triangle ABC,\space P\) and \(Q\) are the mid-points of sides \(AB\) and \(BC\) respectively.

\(PQ\parallel AC,\space PQ=\frac{1}{2}AC\)   (Using mid-point theorem)  ..(1)

In \(\triangle ADC,\space R\) and \(S\) are the mid-points of \(CD\) and \(AD\) respectively.

\(RS\parallel AC,\space RS=\frac{1}{2}AC\) (Using mid-point theorem)  ..(2)

From Equation (1) and (2), we obtain 

\(PQ\parallel RS\) amd PQ=RS\)

It is a parallelogram because one pair of oppositng sides of quadrilateral \(PQRS\) is equal and parallel to each other.  At position \(O\) the diagonals of rhomas \(ABCD\) sholud cross.

In quadrilateral \(OMQN\),

\(MQ\parallel ON\space (PQ\parallel AC)\)

\(QN\parallel OM\space (QR\parallel BD)\)

Hence, \(OMQN\) is a parallelogram

\(∴\angle MQN=\angle NOM\)

\(∴\angle PQR=\angle NOM\)

Since,

\(\angle NOM=90^0\)  (Diagonals of the rhombus are perpendicular to each other)

\(∴ \angle PQR=90^0\)

Clearly, \(PQRS\) is a parallelogram having one of its interior angles as.

So, \(PQRS\) is a rectangle.

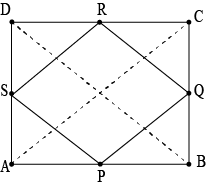
Question 3: \(ABCD\) is a rectangle and \(P,\space Q,\space R\) and \(S\) are mid-points of the sides \(AB,\space BC,\space CD\) and \(DA\) respectively. Show that the quadrilateral \(PQRS\) is a rhombus.

Answer: 

Given: \(ABCD\) is a rectangle and \(P,\space Q,\space R\) and \(S\) are mid-point of the sides \(AB,\space BC,\space CD\) and  \(DA\) respectively.

To prove: The quadrilateral \(PQRS\) is a rhombus.

Let us join \(AC\) and \(BD\)

In \(\triangle ABC,space Q\) are the mid-points of \(AB\) and \(BC\) respectively.

\(PQ\parallel AC\) adn \(PQ=\frac{1}{2}AC\) (Mid-point theorem) ..(1)

Similarly, in \(\triangle ADC,\space SR\parallel AC,\space SR=\frac{1}{2}AC\)  (Mid-point theorem) ..(2)

Clearly, \(PQ\parallel AC\) and \(PQ=SR\)

it is a parallelogram because one pair of opposing sides of quadrilateral \(PQRS\) is equal and parallel to each other.

\(∴PS\parallel QR,\space PS=QR\)  (Opposite sides of parallelogram)  …(3)

In \(\triangle ABC,\space Q\) and \(R\) are the mid-points of sides \(BC\) and \(CD\) respectively.

\(∴QR\parallel BC,\space QR=\frac{1}{2}BD\)  (Mid-point theorem)  …(4)

Also, the diagonals of rectangle are equal.

\(∴AC=BD\)  ..(5)

By using Equations (1), (2), (3), (4) and (5), obtain

\(PQ=QR=SR=PS\)

So \(PQRS\) is a rhombus.

Question 4: \(ABCD\) is a trapezium in which \(AB\parallel DC,\space BD\) is a diagonal and \(E\) is the mid-point of \(AD\). A line is a drawn through \(E\) parallel to \(AB\) intersecting \(BC\) at \(F\) (see the given figure). Show that \(F\) is the mid-point to \(BC\).

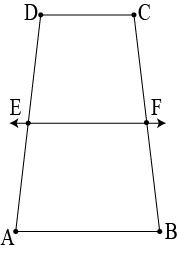
Answer: Given: \(ABCD\) is a trapezium in ehich \(AB\parallel DC,\space BD\) is a fiagonal and \(E\) is the mid-point of \(AD\). A line is drawn throuh \(E\) parallel to \(AB\) intesecting \(BC\) at \(F\).

To prove: \(F\) is the mid-point of \(BC\).

Let \(EF\) inyersect \(DB\) at \(G\)

We know that a line traced through the mid-point of any side of triangle and parallel to another side bisects the third side by the reverse of the mid-point theorem.

In\(\triangle ABD,\space EF\parallel AB\) and \(E\) is the mid-point of \(AD\)

As \(EF\parallel AB,\space AB\parallel CD\),

\(∴EF\parallel CD\) (Two lines parallel to the same line are parallel)

In \(\triangle BCD,\space GF\parallel CD\) and \(G\) is the mid-point of line \(BD\). So, by using converse of mid-point theorem, \(F\) is the mid-point of \(BC\).

Question 5: In a parallelogram \(ABCD,\space E\) and \(F\) are the mid-point of sides \(AB\) and \(CD\) respectively (see the given figure). Show that the line segments \(AF\) and \(EC\) trisect the diagonal \(BD\).

Answer: 

Given: In a parallelogram \(ABCD,\space E\) and \(F\) are the  mid-points of sides \(AB\) and \(CD\) respectively to prove: The line segment \(AF\) and \(EC\) trisect the diagonal \(BD\)

\(ABCD\) is a parallelogram.

\(AB\parallel CD\)

And hence, \(AE\parallel FC\)

Again, \(AB=CD\)  (Opposite sides of parallelogram \(ABCD\))

\(\frac{1}{2}AB=\frac{1}{2}CD\)

\(AE=FC\)  (E and F are mid-points of side AB and CD)

In quadrilateral \(AECF\), one pair of the opposite sides (AE and CF) is parallel and same to each other. So, \(AECF\) is parallelogram.

\(∴AF\parallel EC\)  (Opposite sides of a parellelogram)

In \(\triangle DQC,\space F\) is the mid-point of side \(DC\) and \(FP\parallel CQ\)  (as \(AF\parallel EC\))

So, by using the converse of mid-point theorem, it can be said that \(P\) is the mid-point of \(DQ\).

\(∴DP=OQ\)  ….(1)

Similarly, in \(\triangle APB,\space E\) is the mid-point of side \(AB\) and \(EQ\parallel AP\) (as \(AF\parallel EC\)).

As a result, the reverse of the mid-point theorem may be used to say that \(Q\) is the mid-point of \(PB\)

\(∴PQ=QB\)    ..(2)

From Equation (1) and (2),

\(DP=PQ=BQ\)

Hence, the line segment \(AF\) and \(EC\) trisect the diagonal \(BD\)

Question 6: \(ABC\) is a triangle right angled at \(C\). A line through the mid-point \(M\) of hypotenuse \(AB\) and parallel to \(BC\) intersect \(AC\) at \(D\). Show that

(i) \(D\) is the mid-point of \(AC\)

(ii) \(MD\bot AC\)

(iii) \(CM=Ma=\frac{1}{2}AB\)

Answer: 

Given: \(ABC\) is a triangle right angle at \(C\). A line throught the mid-point \(M\) of hypotenuese \(AB\) and parallel to \(BC\) intersects \(AC\) at \(D\).

To prve: (i) \(D\) is the mid-point of \(AC\)

(ii) \(MD\bot AC\)

(iii) \(CM=MA=\frac{1}{2}AB\)

(i) In \(\triangle ABC\),

it is that \(M\) is athe mid-point of \(AB\) and \(MD\parallel BC\).

Therefore, \(D\) is the mid-point of \(AC\). (Converse of the mid-point theorem)

(ii) As \(MD\parallel CB\) and \(AC\) is a transversal line for them, therefore, (Co-interiro angles)

(iii) join \(MC\).

In \(\triangle AMB\) and \(\triangle CMD\),

\(AD=CD\)  (D is the mid-point of side AC)

\(\angle ADM=\angle CDM\)  (Each)

\(DM=DM\)  (Common)

\(∴\triangle AMD≅\triangle CMD\)  (By SAS congruence rule)

Therefore,

\(AM=CM\)  (By CPCT)

However,

\(AM=\frac{1}{2}AB\)  (M is mid-point of AB)

Therefore, it is said that \(CM=AM=\frac{1}{2}AB\).