NCERT Solutions for Maths Class 9 Chapter 6

EXERCISE 6.1

Question 1 In the given figure, line \(AB\) and \(CD\) interesect at \(O\). If \(\angle AOC+\angle BOE=70^0\) and \(\angle BOD=40^0\) find reflex \(\angle COE\).

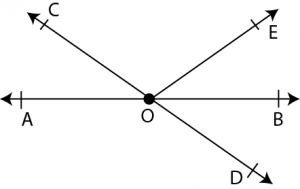
Answer: 

Given: The line \(AB\) and \(CD\) intersect at \(O\).

\(\angle AOC+\angle BOE=70^0\)

\(\angle BOD=40^0\)

And \(AB\) is a straight line: rays n the line are \(OC\) and \(OE\).

If, \(\angle AOC+\angle COE+\angle BOE=180^0\)

\(⇒(\angle AOC+\angle BOE)+\angle COE=180^0\)

\(⇒70^0+\angle COE=180^0\)

\(⇒\angle CO=180^0-70^0=110^0\)

Reflex \(\angle COE=360^0-110^0=250^0\)

∴ Reflex \(\angle COE=250^0\)

Then \(CD\) is a straight line; rays on the ine are \(OE\) and \(OB\).

And \(\angle COE+\angle BOE+\angle BOD=180^0\)

\(⇒110^0+\angle BOE+40^0=180^0\)

\(⇒\angle BOE=180^0-150^0=30^0\)

Hence, \(\angle BOE=30^0\) and Reflex \(\angle COE=250^0\)

Question 2: In the given figure, lines \(XY\) and \(MN\) interesect at \(O\). If \(\angle POy=90^0\) and \(a:b=2:3\), find \(C\).

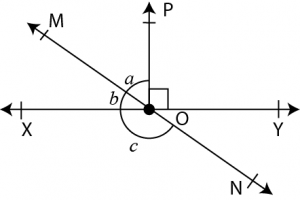
Answer: 

Given The line \(XY\) and \(MN\) intersect at \(O\).

Then, \(\angle POY=90^0\) and \(a:b=2:3\)

Let us assume the common ratio between \(a\) and \(b\) be \(x\).

\(∴a=2x\), and \(b=3x\)

And \(XY\) is a straight line, rays on the line are \(OM\) and \(OP\).

Because \(\angle XOM+\angle MOP+\angle POY=180^0\)

\(b+a+\angle POY=180^0\)

\(3x+2x+90^0=180^0\)

\(5x=90^0\)

\(∴x=180^0\)

Then,

\(a=2x=2\times18=36^0\)

\(b=3x=3\times18=54^0\)

Now, \(MN\) is a straight line. Ray on the line is \(OX\).

The Linear Pair is,

\(b+c=180^0\)

\(54^0+c=180^0\)

\(c=180^0-54^0\)

\(=126^0\)

\(∴c=126^0\)

Question 3: In the given figure, \(\angle PQR=\angle PRQ\), then prove that \(\angle PQS=\angle PRT\)

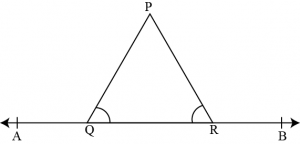
Anwer In the given figure, \(ST\) is a straight line and ray \(QP\) stands on it.

The Linear Pair is.

\(∴\angle PQS+\angle PQR=180^0\)

\(\angle PQR=180^0-\angle PQS\)    …(1)

\(∴\angle PRT+\angle PRQ=180^0\)

\(\angle PRQ=180^0-\angle PRT\)  ..(2)

It is denoted as \(\angle PQR=\angle PRQ\)

Now, equating equations (1) and (2). We get

\(180^0-\angle PQS=180^0-\angle PRT\)

\(∴\angle PQS=\angle PRT\)

Hence proved.

Question 4: In the givn figure, if \(x+y=w+z\) then prove that \(AOB\) is a line.

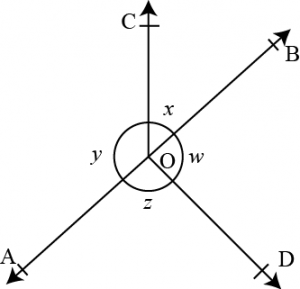
Answer:

Given \(x+y=w+z\).

A complete angle becomes,

\(x+y+z+w=360^0\)

The

\(x+y+x+y=360^0\)

\(2(x+y)=360^0\)

\(∴x+y=180^0\)

Since \(x\) and \(y\) form a linear pair, therefore, \(AOB\) is a line.

Hence proved.

Question 5: In the given figure, \(POQ\) is a line. Ray \(OR\) is perpendicular to line \(PQ\). \(OS\) is another ray lying between rays \(OP\) and \(OR\). Prove that \(\angle ROS=\frac{1}{2}(\angle QOS-\angle POS)\)

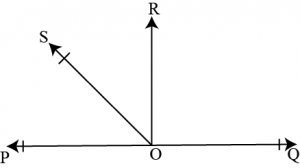
Answer: 

Given \(OR\bot PQ\)

\(\angle POR=90^0\)

\(\angle POS+\angle SOR=90^0\)

\(\angle ROS=90^0+\angle POS\)   …(1)

Because \(OR\bot PQ\) Then,

\(\angle QOR=90^0\)

\(\angle QOS-\angle ROS=90^0\)

\(\angle ROS=\angle QOS-90^0\)     …(2)

Add equation (1) and (2), we obtain

\(2\angle ROS=\angle QOS-\angle POS\)

Hence proved.

Question 6: It is given that \(\angle XYZ=64^0\) and \(XY\) is produced to point \(P\). Draw a figure from the given information. If ray \(YQ\) bisects \(\angle ZYP\), find \(\angle XYQ\) and reflex \(angle QYP\).

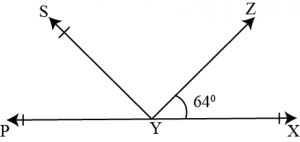
Answer: 

Given: the line \(YQ\) bisects \(\angle PYZ\)

Hence, \(\angle QYP=\angle ZYQ\)

It can be observed that \(PX\) is a line. Rays on the line are \(YQ\) and \(YZ\).

Then, \(\angle XYZ+\angle ZYQ+\angle QYP=180^0\)

\(64+2\angle QYP=180^0\)

\(2\angle QYP=180-64=116\)

\(\angle QYP=58\)

Also, \(\angle ZYQ=\angle QYP=58^0\)

Reflex \(\angle QYP=360^0-58^0=302^0\)

\(\angle XYQ=\angle XYZ+\angle ZYQ\)

\(=64+58=122\)

\(∴\angle XYQ=122\) and Reflex \(\angle QYP=302^0\)

Exercise 6.2

Question 1: In the given figure, find the values of \(x\) and \(y\) and then show that \(AP\parallel CD\).

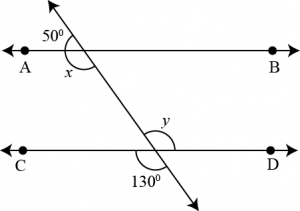
Answer: 

It can be observed that,

By linear pair,

\(50+x=180^0\)

\(∴x=130^0\)

By vertically opposite angles property.

\(y=130\)

A \(x\) and \(y\) are alternate interior angles for line \(AB\) and \(CD\) and also measures of these angles are equal to each other, therefore, line \(AB\parallel CD\).

Hence proved.

Question 2: In the given figure, if \(AB\parallel CD,\space CD\parallel EF\) and \(y:z=3:7\), find \(x\).

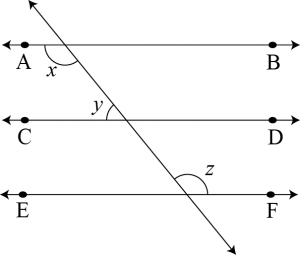
Answer: 

Given \(y:z=3:7,\space AB\parallel CD\) and \(CD\parallel EF\)

If, the lines parallel to the same line are parallel to each other. So,

\(∴AB\parallel CS\parallel EF\)

The alternate interrior angle are equal. Then

\(x=z\)   … (1)

Now, \(y:z=3:7\)

Let us assume that the common ratio between \(y\) and \(z\) be \(a\).

\(∴y=3a\) and \(z=7a\)

Also, co-interior angles on the same side of the transversal. Then,

\(x+y=180^0\)

By equation  (1)

\(z+y=180^0\)

\(7a+3a=180^0\)

\(10a=180^0\)

\(∴a=18^0\)

We get,

\(z=7a\)

\(=7\times18=126^0\)

\(∴x=126^0\)

Question 3: In the figure, if \(AB\parallel CD,\space EF\parallel CD\) and \(\angle GED=126^0\), find \(\angle AGE,\space \angle GEF\) and \(\angle FGE\).

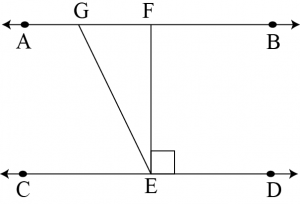
Answer: Give that, \(AB\parallel CD\) and \(EF\parallel CD\). Then,

\(\angle GED=126^0\)

\(\angle GEF+\angle FED=126^0\)

\(\angle GEF+90=126^0\)

\(\angle GEF=36^0\)

As \(\angle AGE\) and \(\angle GED\) are alternate interior angles. We get,

\(\angle AGE=\angle GED=126^0\)

However, by linear pair to obtain \(\angle AGE+\angle FGE=180^0\)

\(126^0+\angle FGE=180^0\)

\(\angle FGE=180^0-126^0=54^0\)

Hence, \(\angle AGE=126^0,\space \angle GEF=26^0\), and \(\angle FGe=54^0\)

Question 4: In the given figure, if \(PQ\parallel ST,\space \angle PQR=110^0\) and \(\angle RST=120^0\), find \(\angle QRS\). [Hint: Draw a line parallel to \(ST\) through point \(R\).]

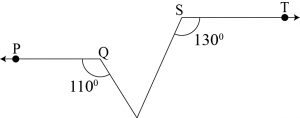
Answer: Given: \(PQ\parallel ST,\space \angle PQR=110\) and \(\angle RST=130^0\)

Now, draw the line \(XY\) parallel to \(ST\) and passing through point \(R\).

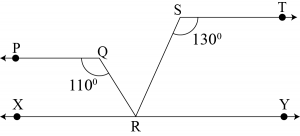
Bym Co-interior angles on the same side of transversal \(QR\). We get,

\(\angle PQR+\angle QRX=180^0\)

\(110^0+\angle QRX=180^0\)

\(\angle QRX=70^0\)

Also, Co-interior angles on the same side of transversal \(SR\) is

\(\angle RST+\angle SRY=180^0\)

\(70+\angle QRS=50=180^0\)

\(\angle QRS=180^0-120^0=60^0\)

\(∴\angle QRS=60^0\)

Question 5: In the given figure, if \(AB\parallel CD,\space \angle APQ=50^0\) and \(\angle PRD=127^0\), find \(x\) and \(y\).

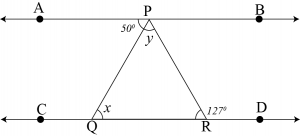
Answer: Alternate interior angle

\(\angle APR=\angle PRD\)

\(50+y=127^0\)

\(y=127^0-50^0\)

\(y=77^0\)

Also,

\(\angle APQ=\angle PQR\)

\(50^0=x\)

\(∴x=50^0\) and \(y-77^0\)

Question 6: In the figure, \(PQ\) and \(RS\) are two mirrors palced parallel to each other. An incident ray \(AB\) strike the mirror \(PQ\) at \(B\), the reflected ray moved along the path \(BC\) and strikes the mirror \(RS\) at \(C\) and again reflects back along \(CD\). Prove tha \(AB\parallel Cd\).

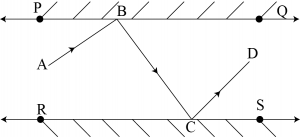
Answer: Let us draw \(BM\bot PQ\) and \(CN\bot RS\).

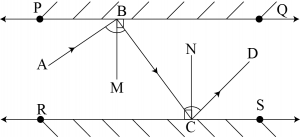
\(∴BM\parallel CN\)

Thus, \(BM\) and \(CN\) are two parallel lines and a transversal line \(BC\) cuts them at \(B\) and \(C\) respectively.

\(\angle 2=\angle 3\)

By laws of reflection we get, \(\angle 1=\angle 2\) and \(\angle3=\angle 4\)

\(\angle 1=\angle2=\angle3=\angle4\)

Also,

\(\angle1+\angle2=\angle3+\angle4\)

\(\angle ABC=\angle DCB\)

Howevere, these are alternate interior angle. Then,

\(∴AB\parallel CD\)

Excercise 6.3

Question 1: In the given figure, sides \(QP\) and \(RQ\) of \(\triangle PQR\) are produced to point \(S\) and \(T\) respectively. If \(\angle SPR=135^0\) and \(PQT=110^0\), find \(\angle PRQ\).

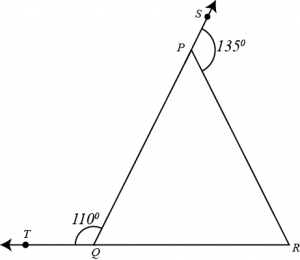
Answer: Given that, \(\angle SPR=135^0\) and \(\angle PQT=110^0\)

By using linear pair angles property, we get,

\(\angle SPR+\angle QPR=180^0\)

\(135^0+\angle QPR=180^0\)

\(∴\angle QPR=45^0\)

Here also use linear pair property.

\(\angle PQT+\angle PQR=180^0\)

\(110+\angle PQR=180^0\)

\(∴\angle PQR=70^0\)

As the sum of all interior angles of a triangles is \(180^0\)

Therefore, for \(\triangle PQR\) we get,

\(\angle QPR+\angle PQR+\angle PRQ=180^0\)

\(45+70+\angle PRQ=180^0\)

\(\angle PRQ=180^0-115^0\)

\(∴\angle PRQ=65^0\)

Question 2: In the figure, \(\angle X=62^0,\space\angle XYZ=54^0\). If \(YO\) and \(ZO\) are the bisects of \(\angle XYZ\) and \(\angle XZY\) respectively of \(\tringle XYZ\), find \(\angle OZY\) and \(\angle YOZ\).

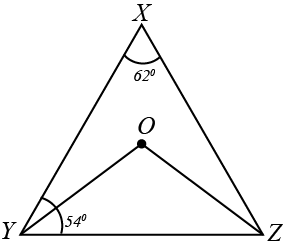
Answer: As the sum of all interior angles of a triangle is \(180^0\).

Therefore, for \(\triangle XYZ\) we get,

\(\angle X+\angle XYZ+\angle XZY=180^0\)

\(62^0+54^0+\angle XZY=180^0\)

\(\angle XZY=180^0-116\)

\(∴\angle XZY=64^0\)

Since, \(OZ\) is the bisector of \(\angle XZY\).

\(\angle OZY=\frac{64}{2}=32^0\)

Similarly, \(\angle OYZ=\frac{54}{2}=27^0\)

Using angle sum property for \(\triangle OYZ\), to obtain

\(\angle OYZ+\angle YOZ+\angle OZY=180^0\)

\(27+\angle YOZ+32=180^0\)

\(\angle YOZ=180^0-59^0\)

\(∴\angle YOZ=121^0\)

Hence, \(\angle OZY=32\) and \(\angle YOZ=121^0\)

Question 3: In the figure, if \(AB\parallel DE,\space \angle BAC=35^0\) and \(\angle CDE=53^0\), find \(\angle DCE\).

Answer: Given: \(AB\parallel DE\)

\(AE\) is a transversal to \(AB\parallel DE\). Then, by alternate interior angles property we get,

\(\angle BAC=\angle CED\)

\(\angle CED=35^0\)

In \(\triangle CDE\), use angle sum property of a triangle, to obtain

\(\angle CDE=35^0\)

\(53^0+35^0+\angle DCE=180^0\)

\(\angle DCE=180^0-88^0\)

\(∴\angle DCE=92^0\)

Question 4: In given figure, if lines \(PQ\) and \(RS\) intersect at point \(T\), such that \(\angle PRT=40^0,\space\angle RPT=95^0\) and \(\angle TSQ=75^0\), find \(\angle SQT\).

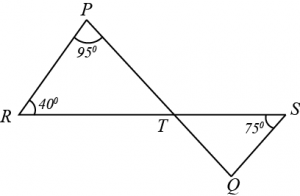
Anwer: Using angle sum property for \(\triangle PRT\), to obtain

\(40^0+95^0+\angle PTR=180^0\)

\(\angle PTR=45^0\)

By using vertically opposite property we get,

\(\angle STQ=\angle PTR=45^0\)

\(∴\angle STQ=45^0\)

Again, using angle sum property for \(\triangle STQ\), to obtain

\(\angle STQ+\angle SQT+\angle QST=180^0\)

\(45+\angle SQT+75^0=180^0\)

\(\angle SQT=180^0-120^0\)

\(∴\angle SQT=60^0\)

Question 5: In the given figure, if \(PQ\bot PS,\space PQ\parallel SR,\space \angle SQR=28^0\) and \(\angle QRT=65^0\) then find the values of \(x\) and \(y\).

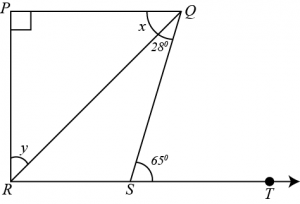
Answer: Given that \(PQ\parallel SR\) and \(QR\) is a transversal line.

By using alternate interior angles property we get,

\(\angle PQR=\angle QRT\)

\(x+28^0=65^0\)

\(x=65^0-28^0\)

\(∴x=37^0\)

By using the angle sum property for \(\triangle SPQ\), to obtain

\(\angle SPQ+x+y=180^0\)

\(90^0+37+y=180^0\)

\(y=180^0-127^0\)

\(∴y=53^0\)

Hence, \(x=37^0\) and \(y=53^0\)

Question 6: In the figure, the side \(QR\) of \(\triangle PQR\) is produced to a point \(S\). If the busectors of \(\angle PQR\) and \(PRS\) meet at point \(T\), then prove that \(\angle QTR=\frac{1}{2}\angle QPR\).

Answer: In \(\triangle QTR,\space \angle TRS\) is an exterior angle.

\(∴\angle QTR+\angle TQR+\angle TRS\)

\(\angle QTR+\angle TRS-\angle TQR\)     …(1)

For \(\triangle PQR,\space \angle PRS\) is an external angle.

\(∴\angle QPR+\angle PQR+\angle PRS\)

As \(QT\) and \(RT\) are angle bisectors. Then,

\(\angle QPR+2\angle TQR=2\angle TRS\)

\(\angle QPR=2(\angle TRS-\angle TQR)\)

By using equation (1), we get,

\(\angle QPR=2\angle QTR\)

\(∴\angle QTR=\frac{1}{2}\angle QPR\)