NCERT Solutions for Maths Class 9 Chapter 3

Chapter 3 – Coordinate Geometry

Exercise – 3.1
Question 1:  How will you describe the position of a table lamp on your study table to another person?
Answer: 
Let us consider the given below figure of a study stable, on which a study lamp is placed.

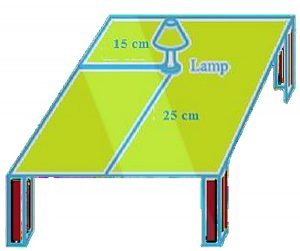
From the above figure,
● Let us consider the lamp on the table as a point
● Let us consider the table as a plane.
● So we can conclude that the table is rectangular in shape, when observed from the top.
▪ The table consists of a short edge and a long edge.

▪ Let us measure the distance of the lamp from the shorter edge and the longer edge.
▪ Let us assume
▪ Distance of the lamp from the shorter edge is 15 cm
▪ Distance of the lamp from the longer edge, its 25 cm.

Therefore, we can conclude that the position of the lamp on the table can be described in two ways depending on the order of the axes as (15, 25) or (25, 15) .

Question 2: (Street Plan): A city has two main roads which cross each other at the center of the city. These two roads are along the North–South direction and East– West direction. All the other streets of the city run parallel to these roads and are 200 m apart. There are 5 streets in each direction. Using 1 cm = 200 m, draw a model of the city on your notebook. Represent the roads/streets by single lines. There are many cross- streets in your model. A particular crossstreet is made by two streets, one running in the North– South direction and another in the East– West direction. Each cross street is referred to in the following  manner: If the 2nd street running in the North–South direction and 5th in the East–West direction meet at some crossing, then we will call this cross-street (2, 5) . Using this convention,
Find:
(i) How many cross – streets can be referred to as (4, 3) .
Answer: 

▪ Draw two perpendicular lines as the two main roads of the city that cross each other at the center.
▪ Mark it as N–S and E–W.
▪ As per given, take scale as 1 cm = 200 m.
▪ Draw five streets that are parallel to both the main roads, to obtain the figure given below:

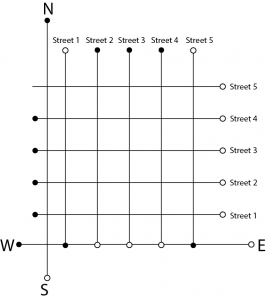
Street plan is as given in the above figure:
∴ There is only one cross street, which can be referred as (4, 3) .
(ii) How many cross – streets can be referred to as (3, 4) .
Answer: 
There is only one cross street, which can be referred as (3, 4) .

Exercise 3.2
1. Write the answer of each of the following questions:
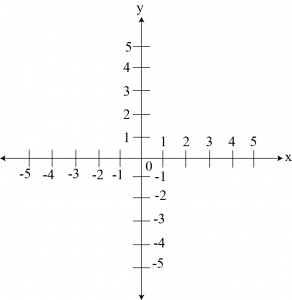
(i) What is the name of horizontal and the vertical lines drawn to determine the position of any point in the Cartesian plane?
Answer: The horizontal line that is drawn to locate the position of any point in the Cartesian plane is called as x -axis. The vertical line that is drawn to locate the position of any point in the Cartesian plane is called as y -axis.

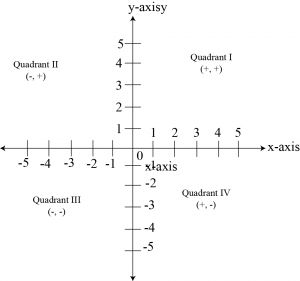
(ii) What is the name of each part of the plane formed by these two lines?
Answer: The each part of the plane made by the x -axis and y -axis is called the quadrants.

(iii) Write the name of the point where these two lines intersect.
Answer: The point where the x -axis and the y -axis meets is called as the origin O).
Question: 2 See the figure, and write the following:

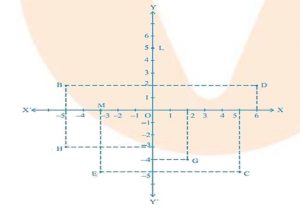
(i) The coordinates of B.
Answser: The coordinates of point \(B\) is the distance of point \(B\) from \(x -\)axis and \(y-\) axis. So, the coordinates of point \(B\) are \((-5,2)\).
(ii) The coordinates of \(C\).
Asnswer: The coordinates of point \(C\) is the distance of point \(C\)  from \(x\) -axis and \(y\) -axis.
So, the coordinates of point \(C\) are \((5,-5)\).
(iii) The point identified by the coordinates \((-3,-5)\).
Answer: The point that represents the coordinates \((-3,-5)\) is \(E\).
(iv) The point identified by the coordinates \((2,-4)\).
Answer: The point that represents the coordinates \((2,-4)\) is \(G\).
(v) The abscissa of the point \(D\).
Answer:  The abscissa of point \(D\) is the distance of point \(D\) from the \(y -\)axis. So, the abscissa of point \(D\) is \(6\).
(vi) The ordinate of the point \(H\).
Answer: The ordinate of point \(H\) is the distance of point \(H\) from the \(x-\)axis.

Therefore, the abscissa of point \(H\) is \(-3\).

(vii) The coordinates of the point \(L\).
Answer: The coordinates of point \(L\) in the above figure is the distance of point \(L\) from \(x -\)axis and \(y -\)axis. So, the coordinates of point \(L\) are \((0.5)\).
(viii) The coordinates of the point \(M\)
Answer: The coordinates of point \(M\) in the above figure is the distance of point \(M\) from \(x-\)axis and \(y -\)axis. So, the coordinates of point \(M\) are \((-3,0)\).