NCERT Solutions for Maths Class 9 Chapter 11

CHAPTER 11

Exercise 11.1:

Question 1: Diameter of the base of a cone is \(10.5\space cm\) and its slant height is \(10\space cm\). Find its curved surface area. [Assume \(\pi=\frac{22}{7}\)]

Answer: 

We are Given the Following:

The slant height \((l)\) of the cone \(=10\space cm\)

The diameter of the base of cone \(=10.5\space cm\)

So, the radius \((r)\) of the base of cone \(=\frac{10.5}{2}\space cm=5.25\space cm\)

The curved surface area of cone, \(A=\pi rl\)

\(⇒A=(\frac{22}{7}\times5.25\times10)\spce cm^2\)

\(⇒A=(22\times0.75\times10)\space cm^2\)

\(⇒A=165\space cm^2\)

Therefore, the curved surface area of the cnde is \(165\space cm^2\)

Question 2: Find the total surface area of a cone, if its slant height is \(21\space m\) and diameter of its base is \(24\space m\) [Assume \(\pi=\frac{22}{7}\)

Answer: 

We are Given The Following:

The slant height \((l)\) of the cone \(=21\space m\)

The diameter of the base of cone \(=24\space m\)

So, the radius (r) of the base of cone \(=\frac{24}{2}m=12\space m\)

The total surface area of cone, \(A=\pi r(1+r\)

\(⇒A=(\frac{22}{7}\times 12\times(21+12))m^2\)

\(⇒A=(\frac{22}{7}\times 12\times 33)m^2\)

\(⇒A=1244.57\space m^2\)

Therefore, the total surface area of cone is \(1244.57\space m^2\)

Question 3: Curved surface area of ac one is \(308\space cm^2\) and its slant height is \(14\space cm\). Find 

i. Radius of the Base.

Answer:

It is given that the slant height \((l)\) of the cone \(=14\space cm\)

The curved surface area of the cone \(308\space cm^2\)

Let us assume the radius of base of cone be \(r\).

We know that curved surface area of the cone \(=\pi rl\)

\(∴\pi rl=208\space cm^2\)

\(⇒(\frac{22}{7}\times r\times 14)cm=308\space cm^2\)

\(⇒r=\frac{308}{44}\space cm\)

\(⇒r=7\space cm\)

Hence, the radius of the base is \(7\space cm\).

(ii) Total Surface area of the cone. [Assume \(\pi=\frac{22}{7}\)]

Answer: The total surface area of the cone is the sum of its curved surface area anf the area of the base.

Total surface area of cone, \(A=\pi rl+\pi r^2\)

\(⇒A=[308+\frac{22}{7}\times (7)^2]cm^2\)

\(⇒A=[308+154]cm^2\)

\{(⇒A=462\space cm^2\)

Hence, the total surface area of the cone is \(462\space cm^2\)

Question 4: A conical tent is \(10\space m\) high and the radius of its base is \(24\space cm\). Find 

i. Slant height of the ten

Answer: 

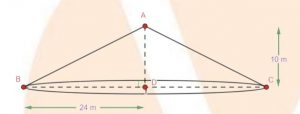
From the figure we can say that \(ABC\) is a conical tent.

It is given that the height \((h)\) of conical tent \(=10\space m\)

The radius \((r)\) of conical tent \(=24\space m\)

Let us assume the slant height as \(1\).

In \(\triangle ABD\), we will use Pythagrean Theorem.

\(∴AB^2=AD^2+BD^2\)

\(⇒1^2=h^2+r^2\)

\(⇒1^2(10\space m)^2+(24\space m)^2\)

\(⇒1^2=676\space m^2\)

\(⇒1=26\space m\)

The slant height of the tent is \(26\space m\).

(ii) cost of canvas required to make the tent, if cost of \(1\space m^2\) canvas is Rs. \(70\). [Assume \(\pi=\frac{22}{7}\)]

Answer: 

The curved surface area of the tent, \(A=\pi rl\)

\(⇒A=(\frac{22}{7}\times24\times26)\space m^2\)

\(⇒A=(\frac{13728}{7})\space m^2\)

It is given that the cost of \(1\space m^2\) of canvas \(=Rs.\space 70\)

So, the cost of \(\frac{13728}{7}\space m^2\) canvas = Rs. \((\frac{13728}{7}\times 70)\) = Rs. \(137280\)

Hence, the cost of canvas requires to make the tent is Rs. 137280\)

Question 5: What length of tarpaulin \(3\space m\) wide will be required to make conical tent of height \(8\space m\) and base radius \(6\space m\)? Assume that the extra length  of material that will be required for stitching margins and wastage in cutting is apporximately \(20\space cm\). [Use \(\pi=3.14\)]

Answer: 

We are given the following:

The base radius (r) of tent = 6 m

The height (h) of the tent = 8 m

So, the slant height of the tent, \(1=\sqrt{r^2+h^2\)

\(⇒1=(\sqrt{6^2+8^2})\space m\)

\(⇒1=(\sqrt{100})\space m\)

\(⇒1=10\space m\)

The curved surface area if the tent, \(A=\pi rl\)

\(⇒A=(3.14\times6\times10)\space m^2\)

\(⇒A=188.4\space m^2\)

It is given that the width of tarpaulin \(=3\space m\)

Let us assume the length of the rapaulin sheet required be \(x\).

It is given that there will be a wastage of \(20\space cm\).

So, ehe new length of the sheet \(=(x-0.2)\space m\)

We know that the area of the ectangular sheet required will be the same as the curved surface area of the tent.

\(∴[(x-0.2)\times 3]\space m=188.4\space m^2\)

\(⇒x-0.2\space m=62.8\space m\)

\(⇒x=63\space m\)

The length of tarpaulin sheet required is \(63\space m\).

Question 6: The slant height and base diameter of a conicall tomb are \(25\space m\) and \(14\space m\) respectively. Find the cost of white-washing its curved surface at the eate of Rs. \(210\) per \(100\space m^2\). [Assume \(\pi=\frac{22}{7}\)]

Answer: 

We are Given the Following:

The base radisu (r) of tomb = 7 m

The slant height (l) of tomb =25 m

The cyrved surface area of the conical tomb, \(A=\pi rl\)

\(⇒A=(\frac{22}{7}\times 7\times25)\space m^2\)

\(⇒A=550\space m^2\)

it is given that the cost of white-washing \(1\space m6w\) area = Rs \(210\)

So, the cost of white-washing \(550\space m^2\) area = Rs. \((\frac{210}{100}\times 550)\) =Rs. \(1155\)

Hence, the cost of white-washing the curved surface arrea of a conical atomb is Rs. \(1155\).

Question 7: A joker’s cap is in the form of a right circular cone of base radisu \(7\space cm\) and the height \(24\space cm\). Find the area of the sheet required to make (10\) such caps. [Assum \(\pi=\frac{22}{7}\)]

Answer: 

We are given the Following:

The base radius (r) of conical cap =7 cm

The height (h) of conical cap = 24 cm

So the slant height of the thent, \(l=\sqrt{r^2+h^2}\)

\(⇒1=(\sqrt{7^2+24^2})\space cm\)

\(⇒1=(\sqrt{625})\space cm\)

\(⇒1=25\space cm\)

The curved surface area of \(10\) conical caps \(=(550\times 10)\space cm^2=5500\space cm^2\)

Therefore, the total area of the sheet required is \(5500\space cm^2\)

Question 8: A bus stop is barricaded from the remaining part of the road, by using 50 hollow conse made of recycled cardboard. Each cone has a base diameter of 40 cm and height 1 m. .If the outer side of each of the conse is to be painred and the cost of painting is Rs. 12 per \(m^2\), what wil be the cost of painting all these conse? [Use \(\pi=3.14\) and take \(\sqt1.04}=1.02\)]

Answer: 

We are given following: 

The ase radius (r) of cone \(=\frac{40}{2}=20\space cm=0.2\space m\)

The height (h) of cone \(=1\space m\)

So, the slant height of the conse, \(1=\sqrt{r^2+h^2}\)

\(⇒1=(\sqrt{(0.2)^2+(1)^2})\space m^2\)

\(⇒1=\sqrt{1.04})\space m\)

\(⇒1=1.02\space m\)

The curved surface area of one cone, \(A=\pi rl\)

\(⇒A=(3.14\times0.2\times1.02)\space m^2\)

\(⇒A=0.64056\space cm^2\)

So, the curved surface area of \(50\) cones \(=(50\times0.64056)\space m^2=32.028\space m^2\)

It is given that the cost of painting \(1\space m^2\) area = Rs. \(12\)

So, the cost of painting \(32.028\space m^2\) aea = Rs. \((32.028\times 12)=Rs.\space 384.336\)

We can also write the cost approximately as \(Rs.\space 384.34\)

Therefore, rhe cost of painting all the hollow cones is \(Rs.\space 384.34\)

Exercise 11.2

[Assume \(\pi=\frac{22}{7}\)], Unless Strated Otherwise

Question 1: Find the surface area of a spehre of radius:

(i) \(10.5\space cm\)

Answer:

Given radius of the sphere \(r=10.5\space cm\)

\(⇒A[4\times\frac{22}{7}\times(10.5)^2]\space cm^2\)

\(⇒A(88\times1.5\times1.5)\space cm^2\)

\(⇒A=1386\space cm^2\)

Hence, the surface area of the sphere is \(1386\space cm^2\).

(ii) \(5.6\space cm\)

Answer: Given radius of the sphere \(r=5.6\space cm\)

The surface area of the sphere \(A=4\space \pi r^2\)

\(⇒A=[4\times\frac{22}{7}\times(5.6)^2]\space cm^2\)

\(⇒A=(88\times0.8\times5.6)\space cm^2\)

\(⇒A=394.24\space cm^2\)

Hence, the surface area of the sphere is \(394.24\space cm^2\)

(iii) \(14\space cm\)

Answer: 

Given radius of the sphere \(r=14\space cm\)

The surface area of the sphere \(A=4\space \pi r^2\)

\(⇒A=[4\times\frac{22}{7}\times(14)^2]\space cm^2\)

\(⇒A=(4\times44\times14)\space cm^2\)

\(⇒A=2646\space cm^2\)

Hence, the surface aera of the sphere is \(2464\space cm^2\)

Question 2: Find the surface area of a sphere of diameter:

(i) \(14\space cm\)

Answer: Given diameter of the sphere \(=14\space cm\)

So, the radius of the sphere \(r=\frac{14}{2}=7\space cm\)

The surface area of the sphere \(A=4\space \pi r^2\)

\(⇒A=[4\times\frac{22}{7}\times(7)^2]\space cm^2\)

\(⇒A=(88\times7\space cm^2\)

\(⇒A=616\space cm^2\)

Hence, the surface area of the sphere is \(616\space cm^2\)

(ii) \(21\space cm\)

Answer: Given diameter of tge sphere \(=21\space cm\)

So, the redius of the sphere \(r=\frac{21}{2}=10.5\space cm\)

The surface area of the sphere \(A=4\space \pi r^2\)

\(⇒A=[4\times\frac{22}{7}\times(10.5)^2]\space cm^2\)

\(⇒A=1386\space cm^2\)

Hence, the sufrace area of the sphere is \(1386\space cm^2\).

(iii) \(3.5\space m\)

Answer: Given diameter of the sphere \(=3.5\space m\)

So, the radius of the sphere \(r=\frac{3.5}{2}=1.75\space m\)

The surface area of the sphere \(A=4\space \pi r^2\)

\(⇒A=[4\times\frac{22}{7}\times(1.75)^2]\space m^2\)

\(⇒A=38.5\space m^2\)

Hence, the surface area of the sphere is \(38.5\space m^2\)

Question 2: Find the total surface area of a hemisphere of radius \(10\space cm\). [Assume \(\pi=\frac{22}{7}\)]

Answer: 

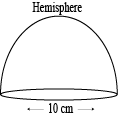
Given the radius of hemisphere \(r=10\space cm\)

The total surface area of the hemisphere is the sum of its curved surface area and the circular base.

Total surface area of hemisphere \(A=2\space \pi r^2+\pi r^2\)

\(⇒A=3\pi r^2\)

\(⇒A=[3\times3.14\times(10)^2]\space cm^2\)

\(⇒A=942\space cm^2\)

Hence, the total surface area of the hemisphere is \(942\space cm^2\).

Question 4: The radius of a spherical balloon increases from 7 cm to 14 cm as air is being pumped into it. Find the ratio of surface areas of the balloon in the two cases.

Answer: Given the intial radius of the balloon \(r_1=10\apce cm\)

The final radius of the balloon \(r_2=14\space cm\)

We have to find the ratio of surface areas of the balloon in the two cases.

The required ratio \(R=\frac{4\space\pi r\space r_^2}{4\space\pi\space r_2^2}\)

\(⇒R=(\frac{r_1}{r_2})^2\)

\(⇒R=(\frac{7}{14})^2\)

\(⇒R=\frac{1}{4}\)

Hence, the ratio of the surface areas of the balloon in both case is \(1:4\).

Question 5: A hemispherical bowl made of brasss has inner diameter \(10.5\space cm\). Find the cost of tinplating it on the inside at the rate of Rs. \(16\) per \(100\space cm^2\).

Answer: Given the radius of inner hemispherical bowl \(r=\frac{10.5}{2}=5.25\space cm\)

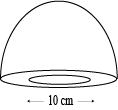
The surface area of the hemispherical bowl A=2\psace\pi\space r^2\)

\(⇒A=[2\times\frac{22}{7}\times(5.25)^2]\space cm^2\)

\(⇒A=173.25\space cm^2\)

It is given that the cost of tin-plating \(100\space cm^2\) area = Rs. \(16\)

So, the cost of tin-plating \(173.25\space cm^2\) area = Rs. \((\frac{16}{100}\times173.25)\) = Rs. \(27.72\)

Hence, the cost of tin-plating the hemispherical bowl ins Rs. \(27.72\).

Question 6: Find the radius of a sphere whose surface area is \(154\space cm^2\).

Answer: Let us assume the radius of sphere be \(r\).

We are given the surface area of the sphere, \(A=154\space cm^2\).

\(∴4\space r^2=154\space cm^2\)

\(⇒r^2=(\frac{154\times7}{2\times11})\space cm^2\)

\(⇒r=(\frac{7}{2})\space cm\)

\(⇒r=3.5\space cm\)

Therefore, the radius of the sphere is \(3.5\) cm.

Question 7: The diameter od the moon is apporximately one-fourth of the diameter of the earth. Find the ratio of their surface area.

Answer: Let us assume the diameter of earth is \(d\).

So, the diameter of the moon will be \(\frac{d}{4}\).

The radius of the earth \(r_1=\frac{d}{2}\)

The radius of the moon \(r_2=\frac{1}{2}\times\frac{d}{2}=\frac{d}{8}\)

The ratio of surface area of moon and earth \(R=\frac{4\space\pi\space r_2^2}{4\space \pi\space r_^2}\)

\(⇒R=\frac{4\space\po(\frac{d}{8})^2}{4\space\pi(\frac{d}{2})^2}\)

\(⇒R=\frac{4}{64}\)

\(⇒=\frac{1}{16}\)

Therefore, the ratio of surface area of moon and earht is \(1:16\)

Question A hemisphericall bowl is made of steel, \(0.25\space cm\) thick. The inner radius if the bowl is \(5\space cm\). Find the outer curved surface area of the bowl.

Answer: 

Given the inner radius \(=5\space cm\)

The thickness of the bow \(=0.25\space cm\)

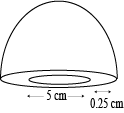
So, the outer radius of the hemispherical bowl is \(r=(5+0.25)\space cm=5.25\space cm\)

The outer curved surface area of the hemispherical bowl \(A=2\space \pi\space r^2\)

\(⇒A=[2\times\frac{2}{7}\times(5.25)^2)\space cm^2\)

\(⇒A=173.25\space cm^2\)

Question 9: A right circular cylinder just encloses a sphere of radius \(r\) (see the below figure). Find 

(i) Surface area of the sphere,

Answer: The surface area of the sphere is \(4\space\pi\space r^2\)

(ii) curved surface area of the cylinder,

Answer:

Given the radius of cylinder \(=r\)

The height of cylinder \(=r+r=2r\)

The curved surface area of cylinder \(A=2\space \pi rh\)

\(⇒A=2\spce\pi\space r(2r)\)

\(⇒A=4\space \pi \space r^2\)

Therefore, the curved surface area of cylinder is \(4\space \pi\space r^2\)

(iii) ratio of the areas obtained in (i) and (ii)

Answer: The raio of surface area of the spehere and curved surface anrea of cylinder \(R=\frac{4\space\pi\space r^2}{4\space\pi\space r^2}\)

\(R=\frac{1}{1}\)

Therefore, the required ratio is \(1:1\)

Exercise 11.3

Question 1: Find the volume of the right circular cone with

(i) Radius \(6\space cm\), height \(7\space cm\)

Answer: It is given the radius of cone \(r=6\space cm\)

The height of the cone \(h=7\space cm\)

The volume of the cone \(V=\frac{1}[3}\pi\space r^2h\)

\(⇒V[\frac{1}{3}\times\frac{22}{7}\times(6)^2\times7]\space cm^3\)

\(⇒V=(12\times22)\space cm^3\)

\(⇒V=264\space cm^3\)

The volume of the right circular cone is \(264\space cm^3\)

(ii) Radius \(3.5\space cm\), height \(12\space cm\) [Assume \(\pi=\frac{22}{7}\)]

Answer: It is given the radius of cone \(r=3.5\space cm\)

The height of the cone \(h=12\space cm\)

The volume of the con \(V=\frac{1}{3}\pi\space r^2h\)

\(⇒V=[\frac{1}{3}\times\frac{22}{7}\times(3.5)^2\times12]\space cm^2\)

\(⇒V=(1.75\times88)\space cm^3\)

\(⇒V=154\space cm^3\)

Question 2: Find the capacity in litres of a conical vessel with 

(i) Radius \(7\space cm\), slant height \(24\space cm\)

Answer: It is given the radius of cone \(r=7\space cm\)

The slant height of the cone \(1=25\space cm\)

So, the height of the cone \(h=\sqrt{1^2-r^2}\)

\(⇒h=\sqrt{25^2-7^2}\space cm\)

\(⇒h=24\space cm\)

The volume of the cone \(V=\frac{1}{3}\space \pi\space r^2h\)

\(⇒V=[\frac{1}{3}\times\frac{22}{7}(7)^2\times24]\space cm^3\)

\(⇒V=(154\times8)\space cm^3\)

\(⇒V=1232\space cm^3\)

We know that \(1000\space cm^3=1\) litre

So, the capacity of the conical vessle \(=\frac{1232}{1000}=1.232\) litres

Therefore, the capacity of the conical vessel is \(1.232\) litres.

(ii) Height \(12\space cm\), slan heigh \(13\space cm\) [Assume \(\pi\frac{22}{7}\)]

Answer: 

It is given the height of cone \(h=12\space cm\)

Tha slant height of the cone \(l=13\space cm\)

So, the radius of the cone \(r=\sqrt{1^2-h^2}\)

\(⇒r=\sqrt{13^2-12^2}\space cm\)

\(⇒r=5\space cm\)

The volume of the cone \(V=\frac{1}{3}\pi\space r^2h\)

\(⇒V=[\frac{1}{3}\times\frac{22}{7}\times(5)^2\times12]\space cm^3\)

\(⇒V=(4\times\frac{22}{7}\times25)\space cm^3\)

\(⇒V=\frac{2200}{7}\space cm^3\)

We know that \(1000\space cm^2=1\) litre

So, the capacity of the conical vessel \(=\frac{2200}{7}\times\frac{1}{1000}=0.314\) litres

Therefore, the capacity of the conical vessel is \(0.314\) litres.

Question 3: The height of a cone is \(15\space cm\). It is volume is \(1570\space cm^3\), find the diamtere of its base. [Use \(\pi=3.14\)]

Answer: it is given the height of cone \(h=12\space cm\)

Let us assume the radius of the cone be \(r\).

The volume of the cone is \(V=1570\space cm^3\)

We know the formula for the volume of the cone \(=\frac{1}{3}\pi\space r^2h\)

\(∴\frac{1}{3}\pi\space r^2h=1570\space cm^3\)

\(⇒[\frac{1}{3}\times\frac{22}{7}\times(r)62\times12]\space =1570\space cm^3\)

\(⇒r^2=100\space cm^2\)

\(⇒r=10\space cm\)

Diameter of bease \(=2r=20\space cm\)

Therefore, the diameter of the cone is \(20\space cm\).

Question 4: If the volume of right circular cone of height \(9\space cm\) is \(48\space\p\space cm^3\), find the diameter of its base.

Answer: It is given the height of cone \(h=9\space cm\)

Let us assume the radius of the cone be \(r\).

The volume of the cone is \(V=48\space \pi\space cm^3\)

We know the formula for the volume of the cone \(=\frac{1}{3}\pi\space r^2h\)

\(∴\frac{1}{3}\pi\space r^2h=48\space \pi\space cm^3\)

\(⇒[\frac{1}{3}\time\pi\times(r)^2\time9]\space cm=48\space \pi\space cm^3\)

\(⇒r^2=16\space cm^2\)

\(⇒r=4\space cm\)

Diameter of base \(=2r=8\space cm\)

Therefore, the diameter of the base of cone is \(8\) cm.

Question 5: A conical pit of top diamter \(3.5\space m\) is \(12\space  m\) deep. What is the capacity in kililitre? [Assume \(\pi=\frac{22}{7}\)]

Answer: It is given the height of conical pit \(=12\space m\)

The radius of conical pit \(r=\frac{3.5}{2}\space m=1.75\space m\)

We know the colume of the conical pit \(V=\frac{1}{3}\pi\space r^2h\)

\(⇒V=[\frac{1}{3}\times\frac{22}{7}\times(1.75)^2\times12]\space m^3\)

\(⇒V=38.5\space m^3\)

We know that \(1\) kilolitre \(=1\space m^3\)

So, the capacity of the pit \(=(38.5\times1)\) kilolitres \(=38.5\) kilolitres.

Therefore, the capacity of the conical pit is \(38.5\) kilolitres.

Question 6: The volume of a right circular cone is \(9856\space cm^3\). If the diameter of the base is \(28\space cm\), find

(i) Height of the cone

Answer: It is given the diameter of base of cone \(=28\space cm\)

So, the radius \(r=\frac{28}{2}=14\space cm\)

Let us assume the height of the cone be \(h\).

The volume of the cone is \(V=9856\space cm^3\)

We know the formula for the volume of the cone \(=\frac{1}{3}\pi\space r^2h\)

\(∴\frac{1}{3}\pi\space r^2h=9856\space cm^3\)

\(⇒[\frac{1}{3}\times\frac{22}{7}\times(14)^2\times h]\space cm^2=9856\space cm^3\)

\(⇒h=(\frac{9856\times21}{22\times196}0\space cm\)

\(⇒h=48\space cm\)

(ii) Slant height of the cone

Answer: The slant heigh of the cone \(1=\sqrt{h^2}r^2}\)

\(⇒1=\sqrt{48^2+14^2}\space cm\)

\(⇒1=\sqrt{2304+196}\space cm\)

\(⇒1=50\space cm\)

Therefore, the slant height of the cone is \(50\space cm\).

(iii) Curved surface area of the cone [Assume \(\pi=\frac{22}{7}\)]

Answer: The curved surface area of the cone \(A=\pi\rl\)

\(⇒A=(\frac{22}{7}\times14\times50)\space cm^2\)

\(⇒A=2200\space cm^2\)

Therefore, the curded surface area of the cone is \(2200\space cm^2\)

Question 7: A right traingle \(\triangla ABC\) with sides \(5\space cm,\space 12\space cm\) and \(13\space cm\) is revolved about the side \(12\space cm\). Find the volume of the solid so obrtained.

Answer: 

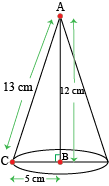
If the triangle is revolved about the side \(12\space cm\), we will get a cone with:

Radius \(r=5\space cm\)

Slant height \(l=13\space cm\)

Height \(h=12\space cm\)

We know the volume of the cone \(V=\frac{1}{l}\pir^2h\)

\(⇒V=[\frac{1}{3}\times\pi\times(5)^2\times12]\space cm^3\)

\(⇒V=100\pi\space cm^3\)

Therefore, the volume of the cone will be \(100\pi\space cm^3\)

Question 8: If the triangle \(\triangle ABC\) in the Question 7 above is revolved about the side \(5\space cm\), the find the volume of the solid so obtained. Find the  ratio of the volumes of the two solids obtained in Question 7 and 8.

Answer: 

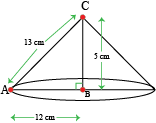
If the triangle is revolved about the side \(5\space cm\), we will get a cone with:

Radius \(r=12\space cm\)

Slant height \(l=13\space cm\)

Height \(h=5\space cm\)

We know the volume of the cone \(V=\frac{1}{3}\pi\space r^2h\)

\(⇒V=[\frac{1}{3}\times\pi\times(12)^2\times5]\space cm^3\)

\(⇒V=240\pi\space cm^3\)

Therefore, the volume of the cone will be \(240\pi\space cm^3\).

The ratio of voume of cone from previus question and the one we obtained above

(=\frac{100\pi}{240\pi}=\frac{5}{12}=5:12\)

Therefore, the required ratio is \(5:12\).

Question 9: A heap of wheat is in the form of a cone whose diameter is \(10.5\space m\) and height is \(3\space m\). Find its volume. The heap is to be covered by canvas to protect it from rain. Find the area of the canvas required. [Assume \(\pi=\frac{22}{7}\)]

Answer: It is  given that diameter of the heap \(=10.5\psace m\)

So, the radius of heap \(r=\frac{10.5}{2}=5.25\space m\)

Height of heap \(h=3\space m\)

We know the volume of the cone \(V=\frac{1}{3}\pi\space r^2h\)

\(⇒V=[\frac{1}{3}\times\frac{22}{7}\times(5.25)^2\times3]\space m^3\)

\(⇒V=86.625\space m^3\)

Hence, the volume of heap is \(86.625\space m^3\)

The area of canvas required is same as curved surface of the cone.

\(∴A=\pi\space rl\)

\(⇒A=\pi r\sqrt{h^2+r^2}\)

\(⇒A=\frac{22}{7}\times5.25\times\sqrt{(3)^2+(5.25)^2}\space m^2\)

\(⇒A={\frac{22}[7}\times5.25\times6.05)\space m^2\)

\(⇒A=99.825\space m^2\)

Therefore, to protect the heap from the rain, the amount of canvas required is \(99.825\space m^2\)