NCERT Solutions for Maths Class 9 Chapter 10
CHAPTER 10
Exercise 10.1:
Question 1: A traffic signal board, indicating ‘SCHOOL AHEAD’, is an equilateral triangle with side ‘a’. Find the area of the signal board, using Heron’s formula. If its perimeter is 180 cm, whatwill be the area of the signal board.
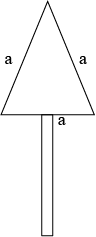
Length of the side of traffic signal board \(=a\)
Perimeter of traffice signal board which is an equilateral triangle \(=3\times a\)
We kno that,
\(2s=\) Perimeter of the triangle,
So, \(2s=3a\)
\(⇒s=\frac{3}{2}\)
Area of triangle can be evaluted by Heron’s formula
\(A=\sqrt{s(s-a)(s-b)(s-c)}\)
Where
\(a,\space b\) and \(c\) are the sides of the triangle
\(s=\frac{a+b+c}{2}\)
Substituting \(s=\frac{3}{2}a\) in Heron’s formula, we get:
Area of given triangle:
\(A=\sqrt{\frac{3}{2}a(\frac{3}{2}a-a)(\frac{3}{2}a-a)(\frac{3}{2}a-a)}\)
\(a=\frac{\sqrt3}{2}a^2\) …(1)
Perimeter of traffice signal board:
\(P=180\space cm\)
Hence, side of traffic signal board
\(a=(\frac{180}{3})\)
\(a=60\) …(2)
Substituting Equation (2) in Equation (1), we get:
Area of traffic signal board is \(A=\frac{\sqrt3}{2}(60\space cm}^2\)
\(⇒A=(\frac{3600}{4}\sqrt3)cm^2\)
\(⇒A=900\sqrt3cm^2\)
Hence, the area of the signal board is \(900\sqrt3\space cm^2\).
Question 2: The triangular side walls of a flyover have been for advertisements. The side of the walls are \(122\space m,\space 22\space m\) and \(12\space m\). The advertisments yield earnings of Rs. 5000\space per\space m^2\) per year. A company hired one of its walls for \(3\) months. How much rent did it pay?

Answer: The length of the sides of the triangle are (say a, b, and c)
\(a=122\space m\)
\(b=22\space m\)
Permeter of triangle = sum of the length of all sides
Perimeter of triangle is:
\(P=122+22+120\)
\(P=264\space m\)
We know that,
\(2s=\) Perimeter of the triangle,
\(2s=264\space m\)
\(s=132\spce m\)
Area of triangle can be evaluated by Heron’s formula:
\(A=\sqrt{s(s-a)(s-b)(s-c)}\)
Where,
\(a,\apce b\) and \(c\) are the sides of the triangle
\(s=\frac{1+b+c}{2}\)
\(s=132\space m\)
Subtituting values of \(s\space a,\space b,\space c\) in Heron’s formula, we get:
Area of given triangle \(=[\sqrt{132(132-122)(132-22)(132-120)}]m^2\)
\(=[\sqrt{132(10)(110)(12)}]m^2=1320\space m^2\)
It is given that:
Rent of \(1\space m^2\) area per years is:
\(R=Rs. 5000/m^2\)
So,
Rent of \(1\space m^2\) area per month will be:
\(R=Rs.\frac{5000}{12}/m^2\)
Rent of \(1320m^2\) area for \(3\) months:
\(R=(\frac{5000}{12}\times3\times1320)/m^2\)
\(⇒R=Rs.1650000\)
Therefore, the total cost rent that company must pay Rs. \(1650000\).
Question 3: There is a slide in a park. One of its side walls has been painted in some colour with a message “KEEP THE PARK GREEN AND CLEAN”. If the sides of the wall are 15 m, 11 m and 6 m, find the area painted in colour.

Answer: It is given that the sides of the wall are \(15\space m,\space 11\space m\) and\(6\space m\).
So, the semi perimeter of triangular wall \((s)=(15+11+6)/2\space m=16\space m\)
Using Heron’s formula,
\(A=\sqrt{s(s-a)(s-b)(s-c)}\)
\(A=\sqrt{16(16-15)(16-11)(16-6}\)
\(A=\sqrt{800}m^2\)
\(A=20\sqrt2m^2\)
Question 4: Find the area of a triangle two sides of which are \(18\space cm\) and \(10\space cm\) adn the perimeter is \(42\space cm\)
Answer: Let the length of the third side of the triangle be \(x\).
Perrimeter of the given triangle:
\(P=42\space cm\)
Let the sides of the triangle be \(a,\space b\) and \(c\).
\(a=18\space cm\)
\(b=10\space cm\)
\(c=x\space cm\)
Perimeter of the triabgle = sum of all sides
\(18+10+x=42\)
\(⇒28x=x=42\)
\(⇒x=14\)
Area of triagle can be evaluated by Heron’s formula:
\(A=\sqrt{s(s-a)(s-b)(s-c)}\)
Where,
\(a\space b\) and \(c\) are the sides of the triangle.
\(s=\frac{a+b+c}{2}\)
\(⇒s=\frac{18+10+14}{2}\)
\(⇒s=21\space cm\)
Substituting values of \(s\space a,\space b,\space\) in Heron’s formula, we get:
Area of given triangle:
\(A=[\sqrt{21(21-18)(21-10)(21-14)}]\)
\(⇒\(A=[\sqrt{21(2)(11)(7)}]\)
\(⇒A=21\sqrt{11}cm^2\)
Hence, the area of the given triangle is \(21\sqrt{11}\space cm^2\)
Question 5: Sides of triangle are in the ration of \(12:17:25\) and its perimeter is \(540\space cm\). Find its area.
Answer: Let the common ratio between the sides of the given traingel be\(x\).
Therefore, the side of the triangle will be \(12x,\space 17x and \(25x\).
It is given that,
Perimetere of this triangle \(=540\space cm\)
Perimeter = sum of the length of all sides
\(12x+17x+25x=540\)
\(⇒54x=540\)
\(⇒x=10\)
Sides of the triangle will be:
\(12\times 10=120\space cm\)
\(17\times10=170\space cm\)
\(25\times10=250\space cm\)
Area of the triangel can be evaluated by Heron’s formula:
\(A=\sqrt{s(s-a)(s-b)(s-c)}\)
Where,
\(a,\space b\) and \(c\) are the sides of the triangle.
\(s=\frac{a+b+c}{2}\)
\(⇒s=\frac{120+170+250}{2}\)
\(⇒s=270\space cm\)
Area of given triangle:
\(A=\sqrt{270(270-120)(270-170)(270-250)}]\)
\(⇒A=[\sqrt{270(150)(100)(2)}]\)
\(⇒A=9000\space cm^2\)
Therefore, the area of this triangle is \(9000\space cm^2\)
Question 6: An isosceles triangle has perimeter 30\space cm\) and each of the equal sides if \(12\space cm\). Find the area of the triangle.
Answer: Let the third side of this traingel be \(x\).
Measure of equal sides if \(12\space cm\) as the given triangle is an isosceles triangle.
It is given that,
Perimeter of triangle, \(P=30\space cm\)
Perimeter of triangle = Sum of the sides
\(12+12+x=30\)
\(⇒c=6\space cm\)
Area of triangle cacn be evaluated by Heron’s formula
\(A=\sqrt{s(s-a)(s-b)(s-c)}\)
Where,
\(a,\space b\) and \(c\) are the sides of the triangle.
\(s=\frac{a+b+c}{2}\)
\(⇒s=\frac{12+12+6}{2}\)
\(⇒s=15\space cm\)
Substituting values of \(s\space a,\space b,\space c\) in Heron’s formula we get:
\(A=[\sqrt{15(15-12)(15-12)(15-6)}]\)
\(⇒S=[\sqrt{15(3)(3)(9)}]\)
\(⇒A=9\sqrt{15}\space cm^2\)
Hence, the area of the given isosceles triangle is \(9\sqrt{15}\space cm^2\)
Study materials
- Refernce Books
- NCERT Solutions
- Syllabus







