NCERT Solutions for Maths Class 9 Chapter 1
Exercise 1.1
Question 1: Do you think zero is a rational number? If it is, then can it be expressed in the form \(\frac{P}{q}\), of where \(p\) and \(q\) are integers an \(q\theta0\) d ? Describe it.
Answer: Remember that, according to the definition of rational number, a rational number is a number that can be expressed in the form of \(\frac{p}{q}\), where and are integers and \(q=\theta\)
Now, notice that zero can be represented as \(\frac{0}{1},\frac{0}{2},\frac{0}{3},\frac{0}{4},\frac{0}{5}………\)
Also, it can be expressed as \(\frac{0}{-1},\frac{0}{-2},\frac{0}{-3},\frac{0}{-4}…….\)
Therefore, it is concluded from here that \(0\) can be expressed in the form of \(\frac{p}{q}\) where \(p\) and \(q\) are integers.
Hence, zero mus be a rational number.
Question 2: Write any 6 rational numbers between 3 and 4.
Answer: It is known that there are infinitely many rational numbers between any two numbers. Since we need to find 6 rational numbers between 3 and 4 , so multiply and divide the numbers by 7 (or by any number greater than 6)
Then it gives,
\(3=3\times\frac{7}{7}=\frac{21}{7}\)
\(4=4\times\frac{7}{7}=\frac{28}{7}\)
Hence, 6 rational numbers found between 3 and 4 are \(\frac{22}{7},\frac{23}{7},\frac{24}{7},\frac{35}{7},\frac{26}{7},\frac{27}{7}\)
Question 3: Write any five rational numbers between \(\frac{3}{5}\) and \(\frac{4}{5}\).
Answer: It is known that there are infinitely many rational numbers between any two numbers.
Since here we need to find five rational numbers between \(\frac{3}{5}\) and \(\frac{4}{5}\), so multiply and divide by 6 (or by number greater than 5)
Then it gives,
\(\frac{3}{5}=\frac{3}{5}\times\frac{6}{6}=\frac{18}{30}\),
\(\frac{4}{5}=\frac{4}{5}\times\frac{6}{6}=\frac{24}{30}\)
Hence, 5 rational numbers found between \(\frac{3}{5}\) and \(\frac{4}{5}\) are \(\frac{19}{30},\frac{20}{30},\frac{21}{30},\frac{22}{30},\frac{23}{30}\)
Question 4: Verify all the statements given below and state whether they are true or false. Show proper reasons for your answers.
(i) Statement: Every natural number is a whole number.
Answer: Write the whole numbers and natural numbers in a separate manner.
It is known that the whole number series is 0,1,2,3,4,5….. . and
the natural number series is 1,2,3,4,5….. .
Therefore, it is concluded that all the natural numbers lie in the whole number
series as represented in the diagram given below.

Thus, it is concluded that every natural number is a whole number.
Hence, the given statement is true.
(ii) Statement: Every integer is a whole number.
Answer: Write the integers and whole numbers in a separate manner.
It is known that integers are those rational numbers that can be expressed in the form of \(\frac{p}{q}\), where \(q=1\).
Now, the series of the integers is like \(0,\pm1,\pm2,\pm3,\pm4,……\)
But the whole numbers are \(0,1,2,3,4,….\)
Therefore, it is seen that all the whole numbers lie within the integer numbers,
but the negative integers are not included in the whole number series.
Thus, it can be concluded from here that every integer is not a whole number.
Hence, the given statement is false.
(iii) Statement: Every rational number is a whole number.
Answer: Write the rational numbers and whole numbers in a separate manner.
It is known that rational numbers are the numbers that can be expressed in the form \(\frac{p}{q}\), where \(q\ne0\) and the whole numbers are represented as \(0,1,2,3,4,5,…….\)
Now notice that every whole number can be expressed in the form of \(\frac{p}{q}\) as \(\frac{0}{1},\frac{1}{1},\frac{2}{1},\frac{3}{1},\frac{4}{1},\frac{5}{1},………\)
Thus, every whole number is a rational number, but all the rational numbers are not whole numbers.
For example,
\(\frac{1}{2},\frac{1}{3},\frac{1}{4},\frac{1}{5},……..\) are not whole numbers.
Therefore, it is concluded from here that every rational number is not a whole number.
Hence, the given statement is false.
Exercise 1.2
Question 1: State whether the following statements are true or false. Justify your answers.
(i) Every irrational number is a real number.
Answer: Write the irrational numbers and the real numbers in a separate manner.
- The irrational numbers and the numbers that cannot be represented in the form \(\frac{p}{q}\), where \(p\) and \(q\) are integers and \(q=\ne0\).
For example, \(\sqrt2,3\pi,.011011011….\) area all irrational numbers.
- The real numb is the collection of both rational numbes and irrational numbers.
For example, \(0,\ne\frac{1}{2}\sqrt2+\pi……\) are all real numbers.
Thus, it is conclueded the every irrational number is a real number.
Hence, the given statement is true.
(ii) Every point on the number line is of the form \(\sqrt{m}\), where \(m\) is a natural number.
Answer: Consider points on a number line to representive well as positive numbers.
Observed that, positive on the number line can be expressed as \(\sqrt1,\sqrt{1.1},\sqrt{1.2},\sqrt{1.3},…….\)
nut any negative number on the number line cannot be expressed as \(\sqrt{-1},\sqrt{-1.1},\sqrt{1.2},\sqrt{1.3},……..\)
because these are not real numbers.
Therefor, it is concluded from here that every number point the number line is not of the form \(\sqrt{m}\), where \(m\) is a natural number.
Hence given statement is false.
(iii) Every real number is an irrational number.
Answer: Write irrational numbes and the real numbers in a separate manner.
- The irrational numbers are the numbers that cannot be repesented in the form \(\frac{p}{q}\) where \(p\) and \(q\) are integers and \(q=\ne0\). For example, \(\sqrt{2},3\pi,.011011011…….\) are all irrational numbers.
- Real numbers are the collection of rational numbers (Ex: \(\frac{1}{2},\frac{2}{3},\frac{3}{5},\frac{5}{7}……\)) and the irrational numbers (Ex: \(\sqrt2,3\pi,.011011011……)\)
Therefore, it can be concluded that every irrational number is a real number, but every real number cannot be an irrational number.
Hence, the given statement is false.
Question 2: Are the square roots of all positive integer numbers irrational? If not, provide an example of the square root of a number that is not an irrational number.
Answer: Square root of every positive integer does not give an integer.
For Example: \(\sqrt2,\sqrt3,\sqrt5,\sqrt6……\) ae not integers, and hence these are irrational numbers. But \(sqrt4\) gives \(\pm2\), these are integers and so, \(\sqrt4\) is not irrational number.
Therefore, it is concluded that the square root of every positive integers is not an irrational number.
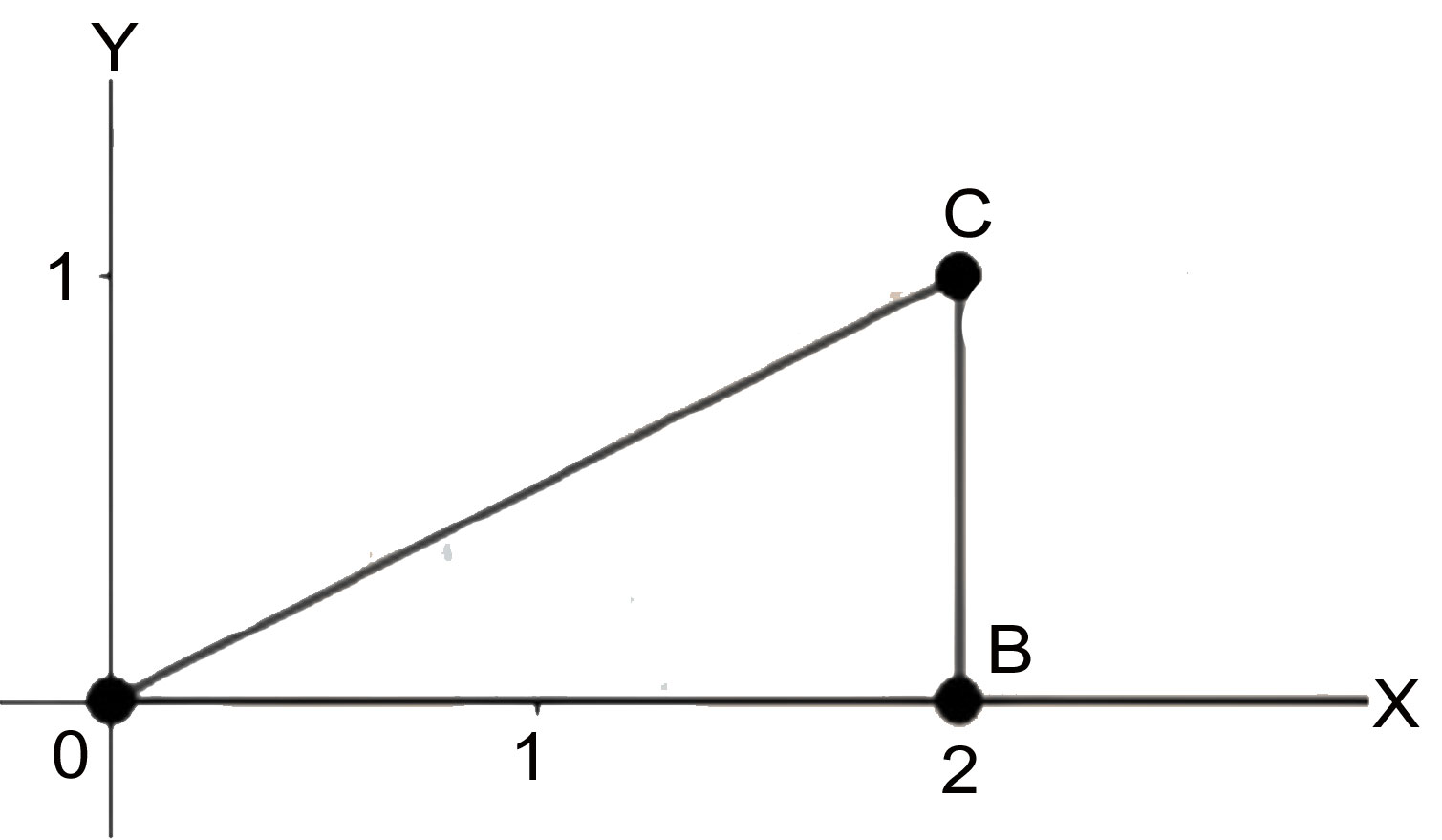
Question 3: Show how \(\sqrt5\) can represented on the number line.
Answer: Follow the procedures to get \(\sqrt5\) on the number line.
- Firstly, Draw a line segment \(AB\) of 2 unit on the number line.
- Secondly, draw a perpendicular line segment \(BC\) at \(B\) of 1 units.
- Thirdly, join the points \(C\) and \(A\), to form a line segment \(AC\0>
- Fourthly, apply the Pythagoras Theorem as
- \(AC^2=AB^2+BC^2\)
- \(AC^2=2^2+1^2\)
- \(AC^2=4+1=5\)
- \(AC=\sqrt5\)
- Finally, draw the arc \(ACD\), to find the number \(\sqrt5\) on the number line as given in the diagram below.
Question 4: Classroom activity (Constructing the ‘square root spiral’):; Take a large sheet of paper and construct the ‘square root spiral’ in the following fashion. Start with a point \(O\) and draw a line segment \(OP_1\) of unit length. Draw a line segment \(P_1\space P_2\) perpendicular to \(OP_1\) of unit length (see Figure). Now draw a line segment \(P_2\space P_3\) perpendicular to \(OP_2\). Then draw a line segment \(P_3\space P_4\) perpendicular to \(OP_3\). Continuing in this manner, you can get the line segment \(P_{n-1}\space P_n\) by drawing a line segment of unit length perpendicular to \(OP{n-1}\). In this manner, you will have created the points \(P_2,P_3,….,P_n,…….,\) and joined them to create a beautiful spiral depicting \(\sqrt2,\sqrt3,\sqrt4,…..\)
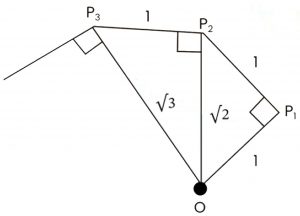

Step 1:Mark a point \(O\)
Choose a point \(O\) on your paper. This will be the center of your square root spiral.
Step 2: Draw line \(OA\) of \(1\space cm\) horizontally.
From point \(O\), draw a straight line \(OA\) horizontally to the right. The length should be \(1\space cm\).
Step 3: Draw perpendicular line \(AB\) of \(1\space cm\)
From point \(A\) (the end of \(OA\)), draw a line \(AB\) certically upwards. The length of \(AB\) should also be \(1\space cm\).
Step 4: Koin \(OB\) (length \(\sqrt2\))
Join point \(O\) to point \(B\) (the end of \(AB\)). The length of \(OB\) should be \(\sqrt2\space cm\).
Step 5: Draw perpendicular line form \(B\) and mark \(C\).
From point \(B\) draw another line perpendicular to \(OB\) (going upwards) of \(1\space cm\). Mark the end point of this line as \(C\).
Step 6: Join \(OC\) (length \(\sqrt3\))
Join point \(O\) to point \(C\). The length of \(OC\) should be \(\sqrt3\space cm\).
Step 7: Repeat the process
Repeat steps 5 and 6 to continue the spiral.
From point \(C\), draw a perpendicular line of \(1\space cm\) upwards and mark the end point as \(D\).
Join \(O\) to \(D\), the length \(OD\) should be \(\sqrt4\space cm\).
Continue this process, each time increasing the length of the perpendicula line by \(1\space cm\) and joining the new point to \(O\) to form the next segment of the spiral, where the length of each segment form \(O\) increases by \(1\) each time (rersulting in \(\sqrt2,\sqrt3,\sqrt4,…..\) etc).
Exercise 1.3
Question 1: Convert the following numbers in decimal form and state what kind of decimal expansion each has:
(i) \(\frac{36}{100}\)
Answer: Divide \(36\) by \(100\).
\(100\begin{vmatrix}\space\space\space36\cr \underline{-0}\end{vmatrix}0.36\)
\({360}\)
\(\underline{-300}\)
\(600\)
\(\underline{-600}\)
\(\underline0\)
So, \(\frac{36}{100}=0.36\) and it is a terminating decimal number.
(ii) \(\frac{1}{11}\)
Answer: Divide \(1\) by \(11\).
\(11\begin{vmatrix}\space\space\space1\cr \underline{-0}\end{vmatrix}0.0909….\)
\({10}\)
\(\underline{-0}\)
\(100\)
\(\underline{-99}\)
\(10\)
\(\underline{-0}\)
\(100\)
\(\underline{-99}\)
\(1\)
It is noticed that while dividing 1 by 11, in the quotient 09 is repeated.
So, \(\frac{1}{11}=0.0909…..\) or
\(\frac{1}{11}=0.\bar{09}\)
and it is a non-terminating and recurring decimal number.
(iii) \(4\frac{1}{8}\)
Answer: \(4\frac{1}{4}=4+\frac{1}{8}\frac{32+1}{8}=\frac{33}{8}\)
Divide 33 by 8.
\(8\begin{vmatrix}\space\space\space33\cr \underline{-32}\end{vmatrix}4.125\)
\({10}\)
\(\underline{-32}\)
\(10\)
\(\underline{-8}\)
\(20\)
\(\underline{-16}\)
\(40\)
\(\underline{-40}\)
\(0\)
Notice that, after dividing 33 by 8, he remainder is found as 0.
So, \(4\frac{1}{8}=4.125\) and it is a terminating decimal number.
(iv) \(\frac{3}{13}\)
\(13\begin{vmatrix}\space\space\space3\cr \underline{-0}\end{vmatrix}0.230769\)
\({30}\)
\(\underline{-26}\)
\(40\)
\(\underline{-39}\)
\(10\)
\(\underline{-0}\)
\(100\)
\(\underline{-91}\)
\(90\)
\(\underline{-78}\)
\(120\)
\(\underline{117}\)
\({3}\)
It is observel that while dividing 3 by 13, the remainder is found as 3 and that is repeated after each 6 continuos divisions.
So, \(\frac{3}{13}=0.230769……\) or
\(\frac{3}{13}=0.\bar{230769}\)
and it is a non-terminating and recuurring decimal number.
(v) \(\frac{2}{11}\)
Answer: Divide 2 by 11.
\(11\begin{vmatrix}\space\space\space2\cr \underline{-0}\end{vmatrix}0.1818…..\)
\({20}\)
\(\underline{-11}\)
\(90\)
\(\underline{-88}\)
\(20\)
\(\underline{-11}\)
\(90\)
\(\underline{-88}\)
\(2\)
It can be noticed that while dividing 2 by 11, the remainder is obtained as 2 and then 9, and these two numbers are repeated infinitelyas remainder.
So, \(\frac{2}{11}=0.1818…..\) or
\(\frac{2}{11}=0.\bar{18}\)
and it is a non-terminating and recurring decimal number.
(vi) \(\frac{329}{400}\)
Answer: Divide 329 by 400.
\(400\begin{vmatrix}\space\space\space329\cr \underline{-0}\end{vmatrix}0.8225\)
\({3290}\)
\(\underline{-3200}\)
\(900\)
\(\underline{-800}\)
\(1000\)
\(\underline{-800}\)
\(2000\)
\(\underline{-2000}\)
\(0\)
It can be seen that while dividing 329 by 400, the remainder is obtained as 0.
So \(\frac{329}{400}=0.8225\) and is a teminating decimal number.
Question 2: If \(\frac{1}{2}=0.142857….\), then predict the decimal expansions of \(\frac{2}{7},\frac{3}{7},\frac{4}{7},\frac{5}{7},\frac{6}{7}\) without calculating the long division?
Answer:
Note that, \(\frac{2}{7},\frac{3}{7},\frac{4}{7},\frac{5}{7}\) and \(\frac{6}{7}\) can be rewritten as\(2\times\frac{1}{7},3\times\frac{1}{7},4\times\frac{1}{7},5\times\frac{1}{7}\) and \(6\times\frac{1}{7}\)
Substituting the value of \(\frac{1}{7}=0.142857\), gives
\(2\times\frac{1}{7}=2\times0.142857…=0.285714…\)
\(3\times\frac{1}{7}=3\times0.428571…=0.4285710…\)
\(4\times\frac{1}{7}=4\times0.142857…=0.571428…\)
\(5\times\frac{1}{7}=5\times0.71425…=0.714285…\)
\(6\times\frac{1}{7}=6\times0.142857..=0.857142…\)
So, the value of \(\frac{2}{7},\frac{3}{7},\frac{4}{7},\frac{5}{7}\) and \(\frac{6}{7}\) obtained without performing long division area
\(\frac{2}{7}=0.\bar{285714}\)
\(\frac{3}{7}=0.\bar{428571}\)
\(\frac{4}{7}=0.\bar{571428}\)
\(\frac{5}{7}=0.\bar{714285}\)
\(\frac{6}{7}=0.\bar{857142}\)
Question 3: Convert the following decimal numbers into the form of \(\frac{p}{q}\), where \(p\) and \(q\) are integers and \(q\ne0\).
(i) \(0.\bar6\)
Answer:
Let \(x=0.\bar6\)
\(⇒c=0.6666\) ….(1)
Multiplying both side of the equation (1) by (10, gives
\(10x=0.6666\times10\)
\(10x=6.6666….\) ..(2)
Subtracting the equation (1) from (2), gives
\(10x=6.6666…\)
\(\underline{-x=0.6666…}\)
\(9x=6\)
\(9x=6\)
\(x=\frac{6}{9}=\frac{2}{3}\)
So, the decimal number becomes
\(0.\bar6=\frac{2}{3}\) and it is in the required \(\frac{p}{q}\) form.
(ii) \(0.\bar{47}\)
Answer:
Let \(x=0.\bar{47}\)
\(⇒x=0.47777….\) …..(a)
Multiplying both sides of the equation (a) by 10, gives
\(10x=4.7777…\) …(b)
Substracting the equation (a) from (b), gives
\(10x=4.7777…\)
\(\underline{-x=0.47777….}\)
\(9x=4.3\)
Therefore,
\(x=\frac{4.3}{9}\times \frac{10}{10}\)
\(⇒x=\frac{43}{90}\)
So, the decimal numbers becomes
\(0.\bar{47}=\frac{43}{90}\) and it is in the required \(\frac{p}{q}\) form.
(iii) \(0.\bar{001}\)
Answer:
Let \(x=0.\bar{001}\) …1
Since the number of rrecurring decimal number is 3, so multiplying booth sides of the equation (1) by 1000, gives
\(1000\times x=1000\times0.001001….\) (2)
Subtracting the equation (1) from (2) gives
\(1000x=1.001001…..\)
\(\underline{x=0.001001….}\)
\(999x=1\)
\(⇒x=\frac{1}{999}\)
Hence, the decimal number becomes.
\(0.\bar001=\frac{1}{99}\) and it is in the \(\frac{p}{q}\) form.
Question 4: Represent the nonterminating decimal number \(0.99999….\) into the form of \(\frac{p}{q}\). Did yiu expect this type of answer? Explain why the answer is appropriate.
Answer:
Let \(x=0.99999….\) …(a)
Multiplying by 10 both sides of the equation (a), gives
\(10x=9.9999….\) ….(b)
Now, subtracting the equation (a) from (b), gives
\(10x=9.99999…..\)
\(\underline{-x=0.99999….}\)
\(9x=9\)
\(⇒x=\frac{9}{9}\)
\(⇒x=1\)
So, the decimal number becomes.
\(0.99999….=\frac{1}{1}\) which is in the \(\frac{p}{q}\) form.
Yes, for a moment we are amazed by our answer, but when we observ that \(0.9999….\) is extending infinitely, then the answer makes sence.
Therefore, there no difference between \(1\) and \(0.9999….\) and hence these two numbers are equal.
Question 5: Find the maximum numbe of digits in the recurring block of digits in the decimal expansion of \(\frac{1}{17}\) by performing the division.
Answer:






