NCERT Solutions for Maths Class 10 Chapter 13
Exercise 13.1
Question 1: 2 cubes each of volume \(64\space cm^3\) are joined end to end. Find the surface area of the resulting cuboids.
Answer:
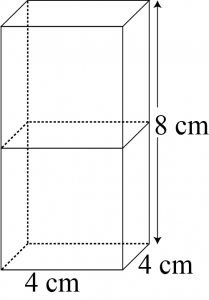
Given that,
Volume of cubes \(= 64\space cm^3\)
\((Edge)^3 = 64\)
\(Edge = 4\space cm\)
If cubes are joined end to end, the dimensions of the resulting cuboid will be \(4\space cm,\space 4\space cm,\space 8\space cm\).
∴ Surface area of cuboids \(=2(lb+bh+lh)\)
\(=2(4×4+4×8+4×8)\)
\(=2(16+32+32)\)
\(=2(16+64)\)
\(=2×80\)
Question 2: A vessel is in the form of a hollow hemisphere mounted by a hollow cylinder. The diameter of the hemisphere is 14 cm and the total height of the vessel is 13 cm.
Find the inner surface area of the vesel. [Use \(\pi=\frac{22}{7}\)]
Answer:
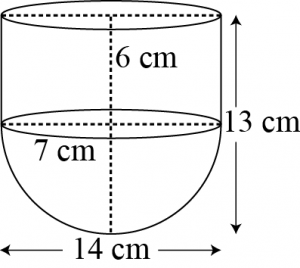
It can be observed that radius \((r)\) of the cylindrical part and the hemispherical part is the same (i.e., \(7\space cm\)).
Height of hemispherical part \(= Radius = 7\space cm\)
Height of cylindrical part \((h) = 13 −7 = 6\space cm\)
Inner surface area of the vessel
\(= CSA\) of cylindrical part \(+ CSA\) of hemispherical part
\(=2\pi r h+2\pi r^2\)
Inner surface area of vessel \(=2×\frac{22}{7}×7×6+2×\frac{22}{7}×7×7\)
\(=44(6+7)=44×13\)
\(=572\space cm^2\)
Question 3: A toy is in the form of a cone of radius 3.5 cm mounted on a hemisphere of same
radius. The total height of the toy is 15.5 cm. Find the total surface area of the toy. [Use \(\pi=\frac{22}{7}\)]
Answer:
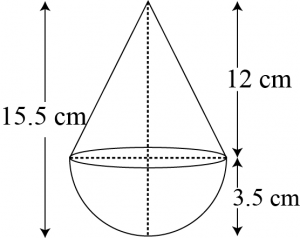
It can be observed that the radius of the conical part
And the hemispherical part is same (i.e., \(3.5\space cm\)).
Height of hemispherical part \(= Radius (r) = 3.5 =\frac{7}{2}\space cm\)
Height of conical part \((h) = 15.5 -3.5 = 12\space cm\)
Slant height \((l)\) of conical part \(=\sqrt{r^2+h^2}\)
\(=\sqrt{(\frac{7}{2})^2+(12)^2}=\sqrt{\frac{49}{4}+44}=\sqrt{\frac{49+575}{4}}\)
\(=\sqrt{\frac{625}{4}}=\frac{25}{2}\)
Total surface area of toy \(=CSA\) of conical part \(+CSA\) of hemispherical part.
\(=\pi l+2\pi r^2\)
\(=\frac{22}{7}\times\frac{7}{2}\times\frac{25}{2}+2\times\frac{22}{7}\times\frac{7}{2}\times\frac{7}{2}\)
\(=137.5+77\)
\(=214.5\space cm^2\)
Question 4: A cubical block of side 7 cm is surmounted by a hemisphere. What is the greatest diameter the hemisphere can have? Find the surface area of the solid. [Use \(\pi=\frac{22}{7}\)]
Answer:
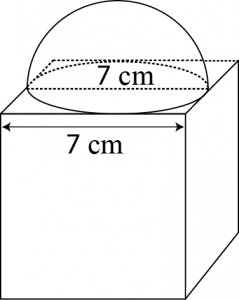
From the figure, it can be observed that the greatest diameter possible for such hemisphere is equal to the cube’s edge, i.e., 7 cm.
Radius \((r)\) of hemispherical part \(=\frac{7}{2}=3.5\space cm\)
Total surface area of solid = Surface area of cubical part + CSA of hemispherical part – Area of base of hemispherical part
\(=6\space (Edge)^2+2\pi r^2=6\space (Edge)^2+\pi r^2\)
Total surface area of solid \(=6(7)^2+\frac{22}{7}\times \frac{7}{2}\times \frac{7}{2}\)
\(=294+38.5\)
\(=332.5\space cm^2\)
Question 5: A hemispherical depression is cut out from one face of a cubical wooden block such that the diameter l of the hemisphere is equal to the edge of the cube. Determine the surface area of the remaining solid.
Answer:
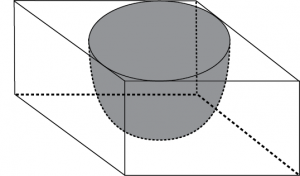
Diameter of hemisphere = Edge of cube \(= l\)
Radius of hemisphere \(= \frac{l}{2}\)
Total surface area of solid = Surface area of cubical-part + CSA of hemispherical part
Area of base of hemispherical part
\(= 6\space (Edge)^2+2\pi r^2-\pi r^2\)
\(=6\space (Edge)^2+\pi r\)
Total surface area of solid \(=6l^2+\pi\times(\frac{l}{2})^2\)
\(=6l^2+\frac{\pi l^2}{4}\)
\(=\frac{1}{4}(24+\pi)l^2\space unit^2\)
Question 6: A medicine capsule is in the shape of cylinder with two hemispheres stuck to each of its ends (see the given figure). The length of the entire capsule is 14 mm and the diameter of the capsule is 5 mm. Find its surface area. [Use \(\pi=\frac{22}{7}\)]
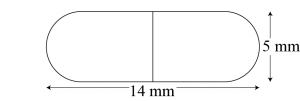
Answer:

It can be observed that
Radius \((r)\) of cylindrical part = Radius \((l)\) of hemispherical part
\(=\frac{Diameter\space of \space the\space capsul}{2}=\frac{5}{2}\)
Length of cylidrical part \((h)\)= Length of the entire capsule \(-2\times r=14-5=9\space cm\)
Surface area of capsule \(=2\times CSA\) of hemispherical part \(+CSA\) of cylindrical part
\(=2×2πr^2+2πrh\)
\(=4π(\frac{5}{2})^2+2π(\frac{5}{2})(9)\)
\(=25π+45π\)
\(=70π mm^2\)
\(=70×\frac{22}{7}\)
\(=220\space mm^2\)
Question 7: A tent is in the shape of a cylinder surmounted by a conical top. If the height and diameter of the cylindrical part are 2.1 m and 4 m respectively, and the slant height of the top is 2.8 m, find the area of the canvas used for making the tent. Also, find the cost of the canvas of the tent at the rate of Rs 500 per m2. (Note that the base of the tent will not be covered with canvas.)
Answer:
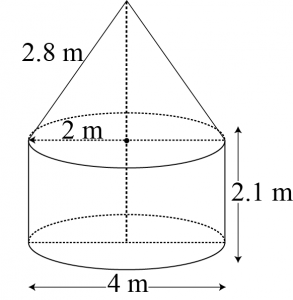
Given that,
Height \((h)\) of the cylindrical part \(= 2.1\space m\)
Diameter of the cylindrical part \(= 4\space m\)
Radius of the cylindrical part \(= 2\space m\)
Slant height \((l)\) of conical part \(= 2.8\space m\)
Area of canvas used
\(=CSA\) of conical part \(+ CSA\) of cylindrical part
\(=πrl+2πrh\)
\(=π×2×2.8+2π×2×2.1\)
\(=2π[2.8+2×2.1]=2π[2.8+4.2]=2×\frac{22}{7}×7\)
\(=44 m^2\)
Cost of \(1\space m^2\) canvas \(= Rs\space 500\)
Cost of \(44\space m^2\) canvas \(= 44 × 500 = 22000\)
Therefore, it will cost \(Rs. 22000\) for making such a tent.
Question 8: From a solid cylinder whose height is 2.4 cm and diameter 1.4 cm, a conical cavity of the same height and same diameter is hollowed out. Find the total surface area of the remaining solid to the nearest cm2.[ Use \(\pi=\frac{22}{7}\)]
Answer:
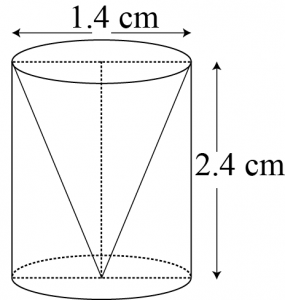
Given that,
Height (h) of the conical part
= Height (h) of the cylindrical part
= 2.4 cm Diameter of the cylindrical part
= 1.4 cm
Therefore, radius (r) of the cylindrical part = 0.7 cm
Slant height (l) of conical part \(=\sqrt{r^2+h^2}\)
\(=\sqrt{(0.7)^2+(2.4)^2}=\sqrt{0.49+5.76}\)
\(=\sqrt{6.25}=2.5\)
Total surface area of the remaining solid will be
\(=CSA\) of cyliderical part \(+CSA\) of conical part \(+\) Area of cylindrical base
\(=2\pi r h+\pi r l+\pi r^2\)
\(=2×\frac{22}{7}×0.7×2.4+\frac{22}{7}×0.7×2.5+\frac{22}{7}×0.7×0.7\)
\(=4.4×2.4+2.2×2.5+2.2×0.7\)
\(=10.56+5.50+1.54=17.60 cm^2\)
The total surface area of the remainig solid to the nearest \(cm^2\) is \(18\space cm^2\).
Question 9: A wooden article was made by scooping out a hemisphere from each end of a solid cylinder, as shown in given figure. If the height of the cylinder is 10 cm, and its base is of radius 3.5 cm, find the total surface area of the article. [ Use \(\pi=\frac{22}{7}\)]
Answer:
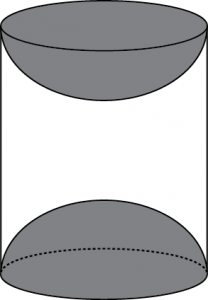
Given that,
Radius (r) of cylindrical part
= Radius (r) of hemispherical part
= 3.5 cm Height of cylindrical part (h)
= 10 cm
Surface area of article
= CSA of cylindrical part + 2 × CSA of hemispherical part
\(=2πrh+2×2πr^2\)
\(=2π×3.5×10+2×2π×3.5×3.5\)
\(=70 π+49π\)
\(=119 π\)
\(=17×22\)
\(=374 cm^2\)
Exercise 13.2
Question 1: A solid is in the shape of a cone standing on a hemisphere with both their radii being equal to \(1\space cm\) and the height of the cone is equal to its radius. Find the volume of the solid in terms of \(π\).
Answer:
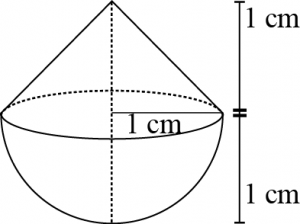
Given that,
Height (h) of conical part
= Radius(r) of conical part = 1 cm
Radius(r) of hemispherical part
= Radius of conical part (r) = 1 cm
Volume of solid
= Volume of conical part + Volume of hemispherical part
\(=\frac{1}{3} πr^2 h+\frac{2}{3}πr^3\)
\(=\frac{1}{3} π(1)^2 (1)+\frac{2}{3} π(1)^3=\frac{π}{3}+\frac{2π}{3}=\frac{3π}{3}=π cm^3\)
Question 2: Rachel, an engineering student, was asked to make a model shaped like a cylinder with two cones attached at its two ends by using a thin aluminum sheet. The diameter of the model is 3 cm and its length is 12 cm. if each cone has a height of 2 cm, find the volume of air contained in the model that Rachel made. (Assume the outer and inner dimensions of the model to be nearly the same.) [Use \(\pi=\frac{22}{7}\)]
Answer:
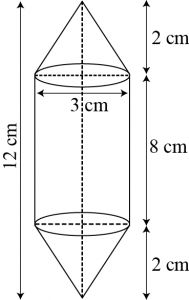
From the figure, it can be observed that
Height \((h_1)\) of each conical part \(= 2\space cm\)
Height \((h_2)\) of cylindrical part \(= 12 − 2 ×\) Height of conical part
\(= 12 − 2 ×2 = 8\space cm\)
Radius \((r)\) of ctlinderical part = Radius of conical part \(=\frac{3}{2}\space cm\)
Volume of air present in the model
= Volume of cylinder \(+2\times\) Volume of cones
\(=\pi r^2+2\times\frac{1}{2}\pi r^2h_1\)
\(=\pi(\frac{3}{2})^2(8)+2\times\frac{1}{3}(\frac{3}{2})^2(2)\)
\(=\pi\times \frac{9}{4}\times\frac{2}{3}\pi\times\frac{9}{4}\times2\)
\(=18\pi+3\pi=21\pi=66\space cm^2\)
Question 3: A gulab jamun, contains sugar syrup up to about 30% of its volume. Find approximately how much syrup would be found in 45 gulab jamuns, each shaped like a cylinder with two hemispherical ends with length 5 cm and diameter 2.8 cm (see the given figure). [Use \(\pi=\frac{22}{7}\)]
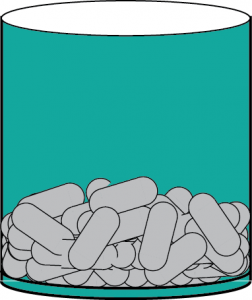
Answer:
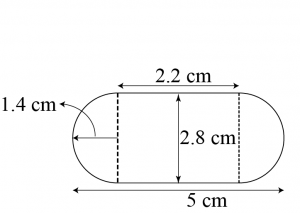
It can be observed that
Radius (r) of cylinderical part = Radius (r) of hemispherical part \(=\frac{2.8}{2}=1.4\space cm\)
Length of each hemispherical part = Radius of hemispherical part = \(1.4\space cm\)
Length (h) of cyliderical part \(=5-2\times\) Length of hemispherical part \(=5-2\times1.4=2.2\space cm\)
Volume of one gulab jammu = Vol. of cylinderical part \(+2\times \) Vol. of hemspherical part
\(=πr^2 h+2×\frac{2}{3} πr^2=πr^2 h+\frac{4}{3} πr^3\)
\(=π×(1.4)^2 2.2+\frac{4}{3} π(1.4)^3\)
\(=\frac{22}{7}×1.4×\frac{1}{4}×2.2+\frac{4}{3}×\frac{22}{7}×1.4×1.4×1.4\)
\(=13.552+11.498=25.05\space cm^3\)
Volume of \(45\) gulab jamuns \(=45×25.05=1,127.25\space cm^3\)
Volume of sugar syrup \(= 30%\) of volume
\(=\frac{30}{100}\times1,1127.25\)
\(338.17\space cm^3\)
\(=338\space cm^3\)
Question 4: A pen stand made of wood is in the shape of a cuboid with four conical depressions to hold pens. The dimensions of the cuboids are 15 cm by 10 cm by 3.5 cm. The radius of each of the depressions is 0.5 cm and the depth is 1.4 cm. Find the volume of wood in the entire stand (see the following figure). [Use \(\pi=\frac{22}{7}\)]

Answer:
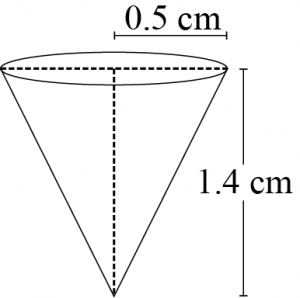
Depth (h) of each conical depression \(= 1.4\space cm\)
Radius (r) of each conical depression \(= 0.5\space cm\)
Volume of wood = Volume of cuboid \(- 4 ×\) Volume of cones
\(=lbh-4×πr^2\space h\)
\(=15×10×3.5-4×\frac{1}{3}×\frac{22}{7}×(\frac{1}{2})^2×1.4\)
\(=525=1.47\)
\(=523.53\space cm^3\)
Question 5: A vessel is in the form of an inverted cone. Its height is 8 cm and the radius of its top, which is open, is 5 cm. It is filled with water up to the brim. When lead shots, each of which is a sphere of radius 0.5 cm are dropped into the vessel, one-fourth of the water flows out. Find the number of lead shots dropped in the vessel.
Answer:
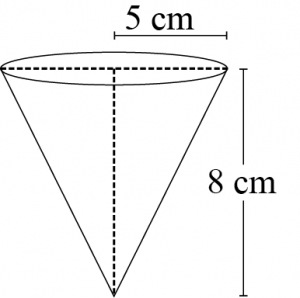
Height (\(h\)) of conical vessel \(= 8\space cm\)
Radius (\(r_1\)) of conical vessel \(= 5\space cm\)
Radius (\(r_2\)) of lead shots \(= 0.5\space cm\)
Let n number of lead shots were dropped in the vessel.
Volume of water spilled = Volume of dropped lead shots
\(\frac{1}{4}\times\) Volume of cone \(=\pi n\times \frac{4}{3}r_2^3\)
\(\frac{1}{4}\times\frac{1}{3}\pi r_1^2=n\times\frac{4}{3}\pi r_2^3\)
Hence, the number of lead shots dropped in the vessel is \(100\).
Question 6: A solid iron pole consists of a cylinder of height 220 cm and base diameter 24 cm, which is surmounted by another cylinder of height 60 cm and radius 8 cm. Find the mass of the pole, given that 1 cm3 of iron has approximately 8 g mass. [Use π = 3.14]
Answer:
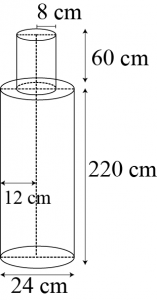
From the figure, it can be observed that
Height (\(h_1\)) of larger cylinder \(=220\space cm\)
Radius (\(r_1\)) of larger cylinder \(=\frac{24}{2}=12\space cm\)
Height (\(h_2\)) of smaller cylinder \(=60\space cm\)
Radius \((r_2)\) of smaller cylinder \(=8\space cm\)
Total volume of pole = Volume of larger cylinder + Volume of smaller cylinder
\(=πr_1^2 h_1+πr_2^2 h_2\)
\(=π(12)^2×220+π(8)^2×60\)
\(=π[144×220+64×60]\)
\(=35520×3.14=1,11,532.8\space cm^2\)
Mass of \(1\space cm^3\) iro \(=8\space g\)
Mass of \(111532.8\space cm^3\) iron \(=111532.8\times8=892262.4\space g=892.262\space kg\)
Question 7: A solid consisting of a right circular cone of height 120 cm and radius 60 cm standing on a hemisphere of radius 60 cm is placed upright in a right circular cylinder full of water such that it touches the bottom. Find the volume of water left in the cylinder, if the radius of the cylinder is 60 cm and its height is 180 cm. [Use \(\pi=\frac{22}{7}\)]
Answer
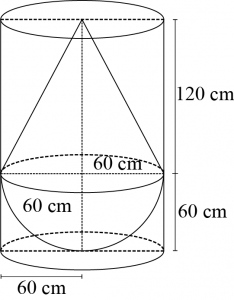
Radius \((r)\) of hemispherical part = Radius \((r)\) of conical part \(= 60\space cm\)
Height \((h_2)\) of conical part of solid \(= 120\space cm\)
Height \((h_1)\) of cylinder \(= 180\space cm\)
Radius \((r)\) of cylinder \(= 60\space cm\)
Volume of water left = Volume of cylinder − Volume of solid
Volume of cylinder –(Volume of cone + Volume of hemisphere)
\(=πr^2 h_1-(\frac{1}{3} πr^2 h_2+\frac{2}{3} πr^3 )\)
\(=π(60)^2 (180)-(1\frac{1}{3}π(60)^2×120+\frac{2}{3}π(60)^3 )\)
\(=π(60)^2 [(180)-(40+40)]\)
\(=π(3.600)(100)=3.60.000π\space cm^3=1131428.l57\space cm^3=1.131\space m^3\)
Question 8: A spherical glass vessel has a cylindrical neck 8 cm long, 2 cm in diameter; the diameter o the spherical part is 8.5 cm. By measuring the amount of water it holds, a child finds its volume to be 345 cm3. Check whether she is correct, taking the above as the inside measurements, and π = 3.14.
Answer:

Height (\(h\)) of cylinderical part \(=8\space cm\)
Radius \((r_2)\) of cylindrical part \(=\frac{2}{2}=1\space cm\)
Radius \((r_1)\) spherical part \(=\frac{8.5}{2}=4.25\space cm\)
Volume of vessel = Volume of sphere + Volume of cylinder
\(=\frac{4}{3}πr_1^3+πr_2^2 h\)
\(=\frac{4}{3}π(\frac{8.5}{2})^3+π(1)^2 (8)\)
\(=\frac{4}{3}×3.14×76.765625+3.14\)
\(=321.392+25.12\)
\(=346.512\)
\(=346.51\space cm^3\)
Hence, she is wrong.
Exercise 13.3
Question 1:
A metallic sphere of radius 4.2 cm is melted and recast into the shape of a cylinder of radius 6 cm. Find the height of the cylinder.
Answer:
Radius \((r_1)\) of hemisphere \(= 4.2\space cm\)
Radius \((r_2)\) of cylinder \(= 6\space cm\)
Let the height of the cylinder be \(h\).
The object formed by recasting the hemisphere will be the same in volume.
Volume of sphere = Volume of cylinder
\(\frac{4}{3} πr_1^2=πr_2^2 h\)
\(\frac{4}{3} π(4.2)^3=π(6)^2 h\)
\(\frac{4}{3}×\frac{4.2×4.2×4.2}{36}=h\)
\(h=(1.4)^3=2.74\space cm\)
Hence, the height of the cylinder so formed will be \(2.74\space cm\).
.Question 2: Metallic spheres of radii 6 cm, 8 cm, and 10 cm, respectively, are melted to form a single solid sphere. Find the radius of the resulting sphere.
Answer:
Radius \((r_1)\) of 1st sphere \(= 6\space cm\)
Radius \((r_2)\) of 2nd sphere \(= 8\space cm\)
Radius \((r_3)\) of 3rd sphere \(= 10\space cm\)
Let the radius of the resulting sphere be \(r\).
The object formed by recasting these spheres will be same in volume as the sum of the volumes of these spheres.
\(\frac{4}{3} π[r_1^3+r_2^3+r_3^3 ]=\frac{4}{3} πr^3\)
\(\frac{4}{3} π[6^3+8^3+10^3 ]=\frac{4}{3} πr^3\)
\(r^3=216+512+1000=1728\)
\(r=12\space cm\)
Therefore, the radius of the sphere so formed will be \(12\space cm\).
Question 3: A 20 m deep well with diameter 7 m is dug and the earth from digging is evenly spread out to form a platform 22 m by 14 m. Find the height of the platform. [Use \(\pi=\frac{22}{7}\)]
Answer:
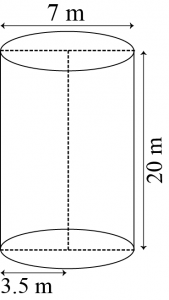
The shape of the well will be cylindrical.
Depth (h) of well = 20 m
Radius (r) of circular end of well = \(\frac{7}{2}\) m.
Area of platform = Length × Breadth = 22 × 14 m2
Let height of the platform = H
Volume of soil dug from the well will be equal to
the volume of soil scattered on the platform.
Volume of soil from well = Volume of soil used to make such platform
\(π×r^2×h=\) Area of platform × Height of platform
\(π×(\frac{7}{2})^2×20=22×14×H\)
\(∴H=\frac{22}{7}×\frac{49}{4}×\frac{2}{22×14}=\frac{5}{2} m=2.5\space m\)
Therefore, the height of such platform will be \(2.5\space m\).
Question 4: A well of diameter 3 m is dug 14 m deep. The earth taken out of it has been spread evenly all around it in the shape of a circular ring of width 4 m to form an embankment. Find the height of the embankment.
Answer:
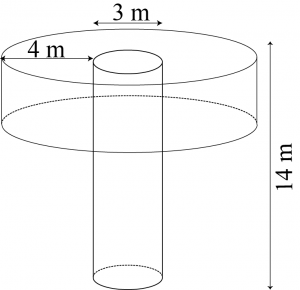
The shape of the well will be cylinderical.
Depth \((h_1)\) of well \(=14\space m\)
Radius \((r_1)\) of the circular end of well \(=\frac{3}{2}\space m\)
Width of embankment \(=4\space m\)
From the figure, it can be observed that our embankment will be in a cylinderical shape having outer radius \((r_2)\) as \(4+\frac{3}{2}=\frac{11}{2}m\)
And inner radius \((r_1)\) as \(\frac{3}{2}\)
Let the height of embankment be \(h_2\).
Volume of soil dug from well = Volume of earth used to form embankment
\(π×r_1^2×h_1=π×(r_2^2-r_1^2 )×h_2\)
\(π×(\frac{3}{2})^2×14π×[(\frac{11}{2})^2-(\frac{3}{2})^2 ]×h\)
\(\frac{9}{4}×14=\frac{112}{4}×h\)
\(h=\frac{9}{8}=1.125\space m\)
Therefore, the height of the embankment will be \(1.125\space m\).
Question 5: A container shaped like a right circular cylinder having diameter 12 cm and height 15 cm is full of ice cream. The ice cream is to be filled into cones of height 12 cm and diameter 6 cm, having a hemispherical shape on the top. Find the number of such cones which can be filled with ice cream.
Answer:
Height (\(h_1\)) of cylindrical container \(= 15\space cm\) Radius
\((r_1)\) of circular end of container \(= \frac{12}{2}=6\space cm\)
Radius (\(r_2\)) of circular end of ice-cream cone \(= \frac{6}{2}=3\space cm\)
Height \((h_2)\) of conical part of ice-cream cone \(= 12\space cm\)
Let n ice-cream cones be filled with ice-cream of the container.
Volume of ice-cream in cylinder \(= n ×\) (Volume of 1 ice-cream cone + Volume of hemispherical shape on the top)
\(πr_1^2 h_1=n(\frac{1}{3} πr_2^2 h_2+\frac{2}{3} πr_2^3 )\)
\(n=\frac{6^2×15}{\frac{1}{3}}×9×12+\frac{2}{3}×(3)^3 \)
\(n=\frac{36×15×3}{108×54}\)
\(n=10\)
Therefore, 10 ice-cream cones can be filled with the ice-cream in the container.
Question 6: How many silver coins, 1.75 cm in diameter and of thickness 2 mm, must be melted to form a cuboid of dimensions \(55.5\space\times10\space cm?\) [Use \(\pi=\frac{22}{7}\)]
Answer:
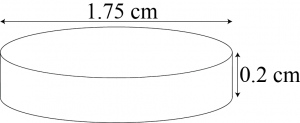
Coins are cylindrical in shape.
Height \((h_1)\) of cylidrical coins \(=2\space mm=0.2\space cm\)
Radius \((r)\) of circular end of coins \(=\frac{1.75}{2}=0.875\space cm\)
Let \(n\) coins be metred to form the required cuboids.
Volume of \(n\) coins = Volume of cuboids
\(n×π×r^2×h_1=l×b×h\)
\(n×π×(0.875)^2×0.2=5.5×10×3.5\)
\(n=\frac{5.5×10×3.5×7}{(0.875)^2×0.2×22}=400\)
Therefore, the number of coins melted to form such a cuboid is \(400\).
Question 7: A cylindrical bucket, 32 cm high and with radius of base 18 cm, is filled with sand. This bucket is emptied on the ground and a conical heap of sand is formed. If the height of the conical heap is 24 cm. Find the radius and slant height of the heap.
Answer:
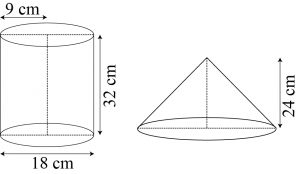
Height \((h_1)\) of cylindrical bucket \(= 32\space cm\)
Radius \((r_1)\) of circular end of bucket \(= 18\space cm\)
Height \((h_2)\) of conical heap \(= 24\space cm\)
Let the radius of the circular end of conical heap be \(r_2\).
The volume of sand in the cylindrical bucket will be equal to the volume of sand in the conical heap.
Volume of sand in the cylindrical bucket = Volume of sand in conical heap
\(π×r_1^2×h_1=\frac{1}{3} π×r_2^2×h_2\)
\(π×18^2×32=\frac{1}{3} π×r_2^2×24\)
\(π×18^2×32=\frac{1}{3}π×r_2^2×24\)
\(r_2^2=\frac{3×18^2×32}{24}18^2×4\)
\(r_2=18×2=36\space cm\)
Slant height \(=\sqrt{36^2+24^2 }=\sqrt{12^2×(3^2×(3^2+2^2)}=12\sqrt{13}\space cm\)
Therefore, the radius and slant height of the conical heap are \(36\space cm\) and \(12\sqrt{13}\space cm\) respectively
Question 8: Water in canal, 6 m wide and 1.5 m deep, is flowing with a speed of 10 km/h. how much area will it irrigate in 30 minutes, if 8 cm of standing water is needed?
Answer:
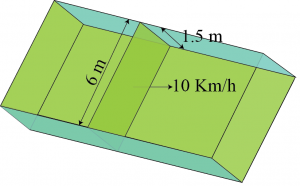
Consider an area of cross-section of canal as \(ABCD\).
Area of cross-section \(= 6 × 1.5 = 9\space m^2\)
Speed of water \(= 10\space km/h = \frac{10000}{60} meter/min\)
Volume of water that flows in 1 minute from canal \(=9×\frac{10000}{6}=1500\space m^3\)
Volume of water that flows in \(30\) minutes from canal \(= 30 × 1500 = 45000\space m^3\)

Let the irrigated area be A. Volume of water irrigating the required area will be equal to the volume of water that flowed in 30 minutes from the canal.
Vol. of water flowing in 30 minutes from canal = Vol. of water irrigating the reqd.
area \(45000=\frac{A\times8}{1000}\)
\(A=562500\space m^2\)
Terefore, area irrigated in \(30\) minutes is \(562500\space m^2\).
Question 9: A farmer connects a pipe of internal diameter 20 cm form a canal into a cylindrical tank in her field, which is 10 m in diameter and 2 m deep. If water flows through the pipe at the rate of 3 km/h, in how much time will the tank be filled?
Answer:

Consider an area of cross-section of pipe as shown in the figure.
Radius \((r_1)\) of circular end of pipe \(=\frac{20}{200}=0.1\space m\)
Area of cross-section \(= π×r_1^2=π×(0.1)^2=0.01π\space m^2\)
Speed of water \(=3\space km/h=\frac{3000}{60}=50\space meter/minute\)
Volume of water that flows in \(1\) minute from pipe \(= 50 ×0.01\space\pi = 0.5π\space m^3\)
Volume of water that flows in t minutes from pipe \(= t × 0.5π\space m^3\)
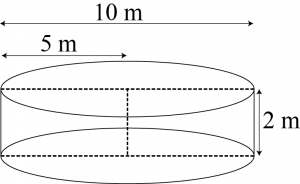
Radius \((r_2)\) of circular end of cylindrical tank \(=\frac{10}{2}=5\space m\)
Depth \((h_2)\) of cylindrical tank \(= 2\space m\)
Let the tank be filled completely in t minutes.
Volume of water filled in tank in t minutes is equal to the volume of water flowed in t minutes from the pipe.
Volume of water that flows in t minutes from pipe = Volume of water in tank
\(t × 0.5π = π ×(r_2)^2 ×h_2\)
\(t × 0.5 =5^2×2\)
\(t = 100\)
Therefore, the cylindrical tank will be filled in \(100\) minutes.
Exercise 13.4
Question 1: A drinking glass is in the shape of a frustum of a cone of height 14 cm. The diameters of its two circular ends are 4 cm and 2 cm. Find the capacity of the glass. [Use \(\pi=\frac{22}{7}\)]
Answer:
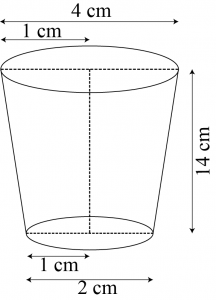
Radius \((r_1)\) of upper \(=\frac{4}{2}=2\space cm\)
Radius \((r_2)\) of lower base of glass \(=\frac{2}{2}=1\space cm\)
Capacity of glass = Volume of frustum of cone
\(=\frac{1}{3}\pi h(r_1^2+r_2^2+r_1r_2)\)
\(=\frac{1}{3}\pi h[(2)^2+(1)^2+(2)(1)]\)
\(=\frac{1}{3}\times\frac{22}{7}\times14[4+1+2]\)
\(=\frac{308}{3}=102\frac{2}{3}\space cm^2\)
Therfore, the capacity of the glass is \(102\frac{2}{3}\space cm^2\)
Question 2: The slant height of a frustum of a cone is 4 cm and the perimeters (circumference) of its circular ends are 18 cm and 6 cm. find the curved surface area of the frustum.
Answer:
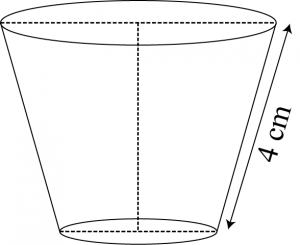
Perimeter of upper circular end of frustum \(= 18 2πr_1 =18\)
\(r_1=\frac{9}{\pi}\)
Perimeter of lower end of frustum \(=6\space cm\)
\(2\pi r_2=6\)
\(r_2=\frac{3}{\pi}\)
Slant height \((l)\) of frustum \(=4\)
\(CSA\) of frustum \(=\pi(r_1+r_2)l\)
\(=\pi(\frac{9}{\pi}+\frac{3}{\pi})4\)
\(=12\times 4\)
\(=48\space cm^2\)
Therefore, the curved surface area of the frustum is \(48\space cm^2\).
Question 3: A fez, the cap used by the Turks, is shaped like the frustum of a cone (see the figure given below). If its radius on the open side is 10 cm, radius at the upper base is 4 cm and its slant height is 15 cm, find the area of material use for making it. [Use \(\pi=\frac{22}{7}\)]

Answer:
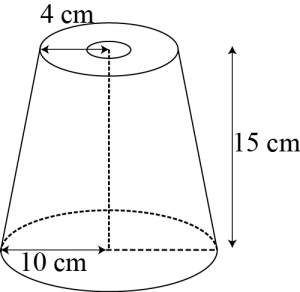
Radius \((r_2)\) at upper circular end \(= 4\space cm\)
Radius \((r_1)\) at lower circular end \(= 10\space cm\)
Slant height \((l)\) of frustum \(= 15\space cm\)
Area of material used for making the fez = CSA of frustum + Area of upper circular end
\(=π(r_1+r_2 )l+πr_2^2\)
\(= π (10 + 4) 15 + π (4)^2\)
\(= π (14) 15 + 16 π\)
\(=210π+16π=\frac{226×22}{7}\)
\(=\frac{710 2}{7}\space cm^2\)
Therefore, the area of material used for making it is \(710 \frac{2}{7}\space cm^2\).
Question 4: A container, opened from the top and made up of a metal sheet, is in the form of a frustum of a cone of height 16 cm with radii of its lower and upper ends as 8 cm and 20 cm respectively. Find the cost of the milk which can completely fill the container, at the rate of Rs.20 per litre. Also find the cost of metal sheet used to make the container, if it costs Rs.8 per \(100\space cm^2\). [Take \(\pi=3.14\)]
Answer:
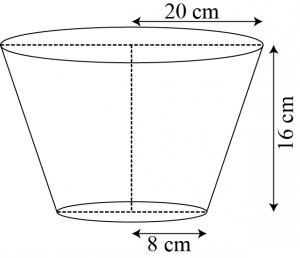
Radius \((r_1)\) of upper end of container \(=20\space cm\)
Radius \((r_2)\) of lower end of caontainer \(=8\space cm\)
Height \((h)\) of container \(=16\space cm\)
Slant height \((l)\) of frustum \(=\sqrt{(r_1-r_2)^2+h^2}\)
\(=\sqrt{(20-8)^2+(16)^2}\)
\(=\sqrt{(12)^2+(16)^2}=\sqrt{144+256}\)
\(=20\space cm\)
Capacity of container = Volume of frustum
\(=\frac{1}{3}\pi h(r_1^2+r_2^2+r_1r_2)\)
\(=\frac{1}{3}\times3.14\times 16\times[(20)^2+(8)^2+(2))(8)]\)
\(=\frac{1}{3}×3.14×16(400+64+160)\)
\(=\frac{1}{3}×3.14×16×624\)
\(=10449.92\space cm^3\)
\(=10.45\) litres.
Cost of \(1\) litre milk \(= Rs\space 20\)
Cost of \(10.45\) litre milk \(= 10.45 × 20\)
\(= Rs\space 209\)
Area of metal sheet used to make the container
\(=π(r_1+r_2 )l+πr_2^2\)
\(= π (20 + 8) 20 + π (8)^2\)
\(= 560 π + 64 π = 624 π\space cm^2\)
Cost of \(1000\space cm^2\) metal sheet \(=Rs\space 8\)
Cost of \(624\space \pi\space cm^2\) metal sheet \(=\frac{624\times3.14\times8}{100}\)
Therefore, the cost of the milk which can completely fill the container is Rs \(209\) and the cost of metal sheet used to make the container is Rs \(156.75\).
Question 5:
A metallic right circular cone 20 cm high and whose vertical angle is \(60^0\) is cut into two parts at the middle of its height by a plane parallel to its base. If the frustum so obtained is drawn into a wire of diameter \(=\frac{1}{16}\space cm\) find the length of the wire. [Use \(\pi=\frac{22}{7}\)]
Answer:
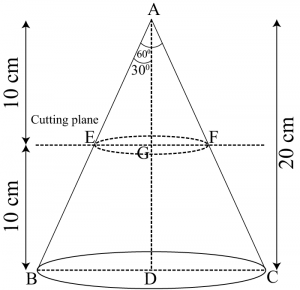
In \(ΔAEG\),
\(\frac{EG}{AG}=tan\space 30^0\)
\(EG=\frac{10}{\sqrt3}cm=\frac{10\sqrt3}{3}\)
In \(ΔABD\),
\(\frac{BD}{AD}=tan\space 30^0\)
\(BD=\frac{20}{\sqrt3}cm=\frac{10\sqrt3}{3}\)
Radius \((r_1)\) of upper end of frustum \(=\frac{10\sqrt3}{3}cm\)
Radius \((r_2)\) of lower end of container \(=\frac{20\sqrt3}{3}cm\)
Height \((h)\) of container \(=10\space cm\)
Volume of frustum \(=\frac{1}{3}\pi h(f_1^2+r_2^2+r_1r_2)\)
\(=\frac{1}{3}\times\pi\times10[(\frac{10\sqrt3}{3})^2+(\frac{20\sqrt3}{3})^2+\frac{(10\sqrt3)(20\sqrt3)}{3\times2}]\)
\(=\frac{10}{3}\pi[\frac{100}{3}+\frac{400}{3}+\frac{200}{3}]\)
\(=\frac{10}{3}\times\frac{22}{7}\times\frac{700}{3}=\frac{22000}{9}cm^3\)
Radius \((r)\) of wire \(=\frac{1}{16}\times\frac{1}{2}=\frac{1}{32}\space cm\)
Let the length of wire be \(l\).
Volume of wire = Area of cross-section\times Length \(=(\pi r^2)(l)\)
\(=(\pi r^2)(l)\)
\(=\pi (\frac{1}{32}^2\times l\)
Volume of frustum = Volume of wire
\(\frac{22000}{9}=\frac{22}{7}\times(\frac{1}{32})^2\times l\)
\(\frac{7000}{9}\times1024=l\)
\(l=796444.44\space cm\)
\(=7964.44\) metres.
Exercise 13.5
Question 1: A copper wire, 3 mm in diameter, is wound about a cylinder whose length is 12 cm, and diameter 10 cm, so as to cover the curved surface of the cylinder. Find the length and mass of the wire, assuming the density of copper to be 8.88 g per cm3.
Answer:
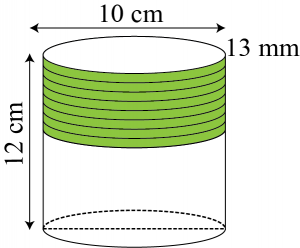
It can be observed that \(1\) round of wire eill cover \(3\space mm\) height of cylinder.
Number of rounds \(=\frac{Height\space of\space cylinder}{Diameter\space of \space wire}\)
\(=\frac{12}{0.3}=40\) rounds
Length of wire required in \(1\) round
= Circumference of base of cylinder
\(=2\pi r=2\pi r\times5=10\pi\)
\(=\frac{400\times22}{7}=\frac{8800}{7}\)
Radius of wire \(=\frac{0.3}{2}=0.15\space cm\)
Volume of wire = Area of cross-section of wire \times Length of wire
\(=\pi(0.15)^2\times1257.14\)
\(=88.898\space cm^2\)
Mass=Volume\(\times\) Density
\(= 88.898 × 8.88\)
\(= 789.41\space gm\)
Question 2: A right triangle whose sides are 3 cm and 4 cm (other than hypotenuse) is made to revolve about its hypotenuse. Find the volume and surface area of the double cone so formed. (Choose value of π as found appropriate.)
Answer:

The double cone so formed by revolving this right-angled triangle \(ABC\) about its hypotenuse is shown in the figure.
Hypotenuse \(AC=\sqrt{3^2+4^2}\)
\(=\sqrt{25}=5\space cm\)
Area of \(ΔABC =\frac{1}{2}×AB×AC\)
\(=\frac{1}{2}×AC×OB=\frac{1}{2}×4×3\)
\(\frac{1}{2}×5×OB=6\)
\(OB=\frac{12}{5}=2.4\space cm\)
Volume of double cone
= Volume of cone \(1 +\) Volume of cone \(2\)
\(=\frac{1}{2} πr^2 h_1+\frac{1}{3}πr^2 h_2\)
\(=\frac{1}{3} πr^2 h_1 (h_1+h_2 )=\frac{1}{3}πr^2 (OA+OC)\)
\(=\frac{1}{3}×3.14×(2.4)^2 (5)\)
\(=30.14\space cm^3\)
Surface area of double cone
= Surface area of cone \(1 + \)Surface area of cone \(2\)
\(= πrl_1 + πr^2\)
\(=πr[4+3]=3.14×2.4×7\)
\(= 52.75 cm^2\)
Question 3: A cistern, internally measuring 150 cm × 120 cm × 110 cm, has 129600 cm3 of water in it. Porous bricks are placed in the water until the cistern is full to the brim. Each brick absorbs one-seventeenth of its own volume of water. How many bricks can be put in without overflowing the water, each brick being 22.5 cm × 7.5 cm × 6.5 cm?
Answer:
Volume of cistern = 150 × 120 × 110 = 1980000 cm3
Volume to be filled in cistern = 1980000 − 129600 = 1850400 cm3
Let n numbers of porous bricks were placed in the cistern.
Volume of n bricks = n × 22.5 × 7.5 × 6.5 = 1096.875n
As each brick absorbs one-seventeenth of its volume,
Therefore, volume absorbed by these bricks \(=\frac{n}{17}(1096.875)\)
\(1850400+\frac{n}{17} (1096.875)=(1096.875)n\)
\(1850400=\frac{16n}{17}(1096.875)\)
\(n = 1792.41\)
Therefore, \(1792\) bricks were placed in the cistern.
Question 5: An oil funnel made of tin sheet consists of a 10 cm long cylindrical portion attached to a frustum of a cone. If the total height is 22 cm, diameter of the cylindrical portion is 8 cm and the diameter of the top of the funnel is 18 cm, find the area of the tin sheet required to make the funnel (see the given figure).
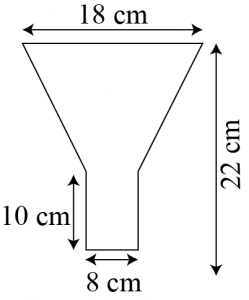
Answer:
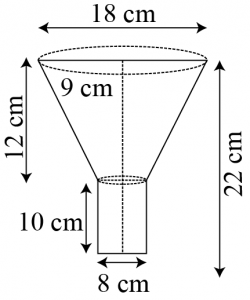
Radius (r1) of upper circular end of frustum part \(=\frac{18}{2}=9\space cm\)
Radius (r2) of lower circular end of frustum part
= Radius of circular end of cylindrical part \(\frac{8}{2}=4\space cm\)
Height (h1) of frustum part\(= 22 – 10 = 12\space cm\)
Height (h2) of cylindrical part \(= 10\space cm\)
Slant height (l) of frustum part
\(=\sqrt{(r_1-r_2)^2}=\sqrt{(9-4)^2+(12)^2}=13\space cm\)
Area of tin sheet required
CSA of frustum part + CSA of cylinderical part
\(=π(r_1+r_2 )l+2π_2 h_2\)
\(=\frac{22}{7} [169+80]=\frac{22×249}{7}\)
\(=\frac{782 4}{7}\)
Question 6:
Derive the formula for the curved surface area and total surface area of the frustum of cone.
Answer:
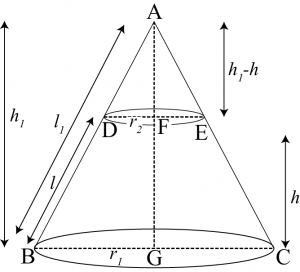
Let ABC be a cone. A frustum DECB is cut by a plane parallel to its base. Let r1 and r2 be the radii of the ends of the frustum of the cone and h be the height of the frustum of the cone.
In ΔABG and ΔADF, DF||BG
\(∴ ΔABG ∼ ΔADF\)
\(\frac{DF}{BG}=\frac{AF}{AG}=\frac{AD}{AB}\)
\(\frac{r_2}{r_1}=\frac{h_1-h}{h_1}-\frac{l_1-l}{l_1}\)
\(\frac{r_2}{l_1}=l-\frac{h}{h_1}=1-\frac{l}{l_1}\)
\(1-\frac{l}{l_1}=\frac{r_2}{r_1}\)
\(\frac{l}{l_1}=\frac{1r_2}{r_1}=\frac{r_1-r_2}{r_1}\)
\(\frac{l_1}{l}=\frac{r}{r_1-r_2}\)
\(l_1=\frac{r_1l}{r_1-r_2}\)
CSA of frustum \(DECB=CSA\) of cone \(ABC-CSA\) cone \(ADE\)
\(=πr_1 l_1-πr_2 (l_1-l)\)
\(=πr_1(\frac{lr_1}{r_1-r_2})-πr_2[\frac{r_1l}{r_1-r_2}-l]\)
\(=\frac{πr_1^2l}{r_1-r_2}=πr_2(\frac{r_1l-r_1l+r_2l}{r_1-r_2})\)
\(=\frac{πr_1^2l}{r_1-r_2}-\frac{πr_2^2l}{r_1-r_2}\)
\(=πl[\frac{r_1^2-r_2^2}{r_1-r_2}]\)
CSA of frustum \(=π(r_1+r_2)l\)
Total surface area of frustum =CSA frustum + Area of upper circular end + Area of lower circular end
\(=π(r_1+r_2 )l+πr_2^2+πr_1^2\)
\(=π[(r_1+r_2 )l+r_1^2+r_2^2 ]\)
Question 7: Derive the formula for the volume of the frustum of a cone.
Answer:
Let ABC be a cone. A frustum DECB is cut by a plane parallel to its base.
Let \(r_1\) and \(r_2\) be the radii of the ends of the frustum of the cone and \(h\) be the height of the frustum of the cone.
In \(ΔABG\) and \(ΔADF, DF||BG\)
\(∴ ΔABG ∼ ΔADF\)
\(\frac{BF}{BG}=\frac{AF}{AG}=\frac{AD}{AB}\)
\(\frac{r_2}{r_1}=\frac{h_1-h}{h_1}=\frac{l_1-l}{l_1}\)
\(\frac{r_2}{r_1}=1-\frac{h}{h_1}=1-\frac{l}{l_1}\)
\(1-\frac{l}{l_1}=\frac{r_2}{r_1}\)
\(\frac{h}{h_1}=1-\frac{r_2}{r_1}=\frac{r_1-r_2}{r_1}\)
\(\frac{h_1}{h}=\frac{r_1}{r_1-r_2}\)
\(h_1=\frac{r_1h}{r_1-r_2}\)
Volume of frustum of cone = Volume of cone \(ABC\)− Volume of cone \(ADE\)
\(=\frac{1}{3} π_1^2 h_1-\frac{1}{3} πr_2^2 (h_1-h)\)
\(=\frac{π}{3} [r_1^2 h_1-r_2^2 (h_1-h)]\)
\(=\frac{π}{3} [r_1^2 (\frac{hr_1}{r_1-r_2 })-r_2^2 (\frac{hr_1}{r_1-r_2 }-h)]\)
\( =\frac{π}{3} [(\frac{hr_1^3}{r_1-r_2 })-r_2^2 (\frac{hr_1-hr_1+hr_2}{r_1-r_2})]\)
\(=\frac{π}{3} [\frac{hr_1^3}{r_1-r_2}-\frac{hr_2^3}{r_1-r_2 }]\)
\(=\frac{π}{3} h[\frac{r_1^3-r_2^3}{r_1-r_2 }]\)
\(=\frac{π}{3} h[\frac{(r_1-r_2)(r_1^2+r_2^2+r_1 r_2)}{r_1-r_2}]\)
\(=\frac{1}{3}πh[r_1^2+r_2^2+r_1 r_2 ]\)
Study materials
- Refernce Books
- NCERT Solutions
- Syllabus







