NCERT Solutions for Maths Class 10 Chapter 10

Exercise 10.2

Question 1: From a point \(Q\), the length of the tangent to a circle is \(24\space cm\) and the distance of \(Q\) from the centre is \(25\space cm\). The radius of the circle is

(a) \(7\space cm\)

(b) \(12\space cm\)     

(c)  \(15\space cm\)

(d) \(24.5\space cm\)

Answer:

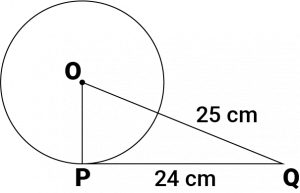
Let \(O\) be the centre of the circle.
Given that,

\(OQ = 25\space cm\) and \(PQ = 24\space cm\)

As the radius is perpendicular to the tangent at the point of contact,

Therefore, \(OP ⊥ PQ\)

Applying Pythagoras theorem in \(ΔOPQ\), we obtain

\(OP^0 + PQ^2 = OQ^2\)

\(OP^2 + 24^2 = 25^2\)
\(OP^2 = 625 − 576\)
\(OP^2 = 49\)

\(OP = 7\)

Therefore, the radius of the circle is \(7\space cm\).
Hence, alternative (a) is correct

Question 2: In the given figure, if \(TP\) and \(TQ\) are the two tangents to a circle with centre \(O\) so that \(∠POQ = 110^0\), then \(∠PTQ\) is equal to

(a) \(60^0\)

(b) \(70^0\)

(c) \(80^0\)

(d) \(90^0\)

Answer: 

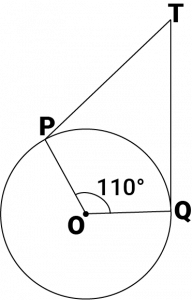
It is given that \(TP\) and \(TQ\) are tangents.

Therefore, radius drawn to these tangents will be perpendicular to the tangents.

Thus, \(OP ⊥ TP\) and \(OQ ⊥ TQ\)

\(∠OPT = 90^0\)

\(∠OQT = 90^0\)

In quadrilateral \(POQT\),

Sum of all interior angles \(= 360^0\)

\(∠OPT + ∠POQ +∠OQT + ∠PTQ = 360^0\)
\(⇒ 90^0+ 110^0 + 90^0+∠PTQ = 360^0\)

\(⇒ PTQ = 70^0\)  

Question 3: If tangents \(PA\)  and \(PB\) from a point \(P\) to a circle with centre \(O\) are inclined to each other an angle of \(80^0\), then \(∠POA\) is equal to 

(a) \(50^0\)

(b) \(60^0\)

(c) \(70^0\)

(d) \(80^0\)

Answer: 

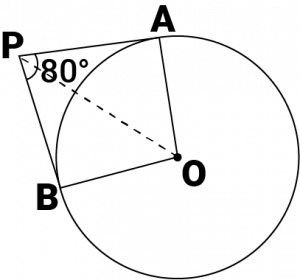
Answer: It is given that \(PA\) and \(PB\) are tangents.

Therefore, the radius drawn to these tangents will be perpendicular to the tangents.

Thus, \(OA ⊥ PA\) and \(OB ⊥ PB\)

\(∠OBP = 90^0\)

\(∠OAP = 90^0\)
In \(AOBP\),

Sum of all interior angles \(= 360^0\)

\(∠OAP + ∠APB +∠PBO + ∠BOA = 360^0\)
\(90^0+ 80^0+90^0 + BOA = 360^0\)
\(∠BOA = 100\)

In \(ΔOPB\) and \(ΔOPA\),

\(AP = BP\) (Tangents from a point)
\(OA = OB\) (Radii of the circle)
\(OP = OP\) (Common side)

Therefore, \(ΔOPB ≅ ΔOPA\) (SSS congruence criterion)

\(A ↔ B, P ↔ P, O ↔ O\)

And thus, \(∠POB = ∠POA\)

\(\angle POA=\frac{1}{2}\angle AOB=\frac{100^0}{2}=50^0\)

Question 4: Prove that the tangents drawn at the ends of a diameter of a circle are parallel.

Answer:

Let \(AB\) be a diameter of the circle.

Two tangents \(PQ\) and \(RS\) are drawn at points \(A\) and \(B\) respectively.

Radius drawn to these tangents will be perpendicular to the tangents.

Thus, \(OA ⊥ RS\) and \(OB ⊥ PQ\)

\(∠OAR = 90^0\)

\(∠OAS = 90^0\)
\(∠OBP = 90^0\)
\(∠OBQ = 90^0\)

It can be observed that

\(∠OAR = ∠OBQ\) (Alternate interior angles)
\(∠OAS = ∠OBP\) (Alternate interior angles)

Since alternate interior angles are equal, lines \(PQ\) and \(RS\) will be parallel.

Question 5:  Prove that the perpendicular at the point of contact to the tangent to a circle passes through the centre.

Answer:

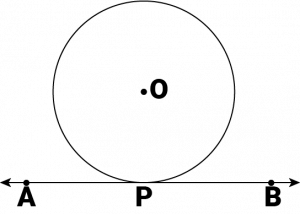
Let us consider a circle with centre \(O\).

Let \(AB\) be a tangent which touches the circle at \(P\).

We have to prove that the line perpendicular to \(AB\) at P passes through centre \(O\).

We shall prove this by contradiction method.

Let us assume that the perpendicular to \(AB\) at \(P\) does not pass through centre \(O\).

Let it pass through another point \(O’\). Join \(OP\) and \(O’P\).

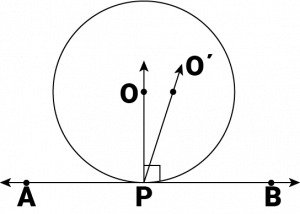
As perpendicular to \(AB\) at \(P\) passes through \(O’\), therefore, \(∠O’PB = 90^0\)  … (1)

\(O\) is the centre of the circle and \(P\) is the point of contact. We know the line joining the centre and the point of contact to the tangent of the circle are perpendicular to each other.

\(∴ ∠OPB = 90^0\) … (2)

Comparing equations (1) and (2), we obtain \(∠O’PB = ∠OPB\) … (3)

From the figure, it can be observed that,
\(∠O’PB < ∠OPB\) … (4)

Therefore, \(∠O’PB = ∠OPB\) is not possible. It is only possible, when the line \(O’P\) coincides with \(OP\).

Therefore, the perpendicular to \(AB\) through \(P\) passes through centre \(O\).

Question 6: The length of a tangent from a point \(A\) at distance \(5\space cm\) from the centre of the circle is \(4\space cm\). Find the radius of the circle.

Answer:

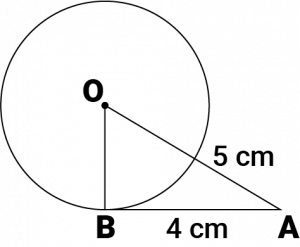
Let us consider a circle centered at point \(O\).

\(AB\) is a tangent drawn on this circle from point \(A\). Given that,

\(OA = 5\space cm\) and \(AB = 4\space cm\)
In \(ΔABO\),

\(OB ⊥ AB\) (Radius ⊥ tangent at the point of contact)

Applying Pythagoras theorem in \(ΔABO\), we obtain \(AB^2 + BO^2 = OA^2\)

\(4^2 + BO^2 = 5^2\)
\(16 + BO2 = 25\)
\(BO^2 = 9\)

\(BO = 3\)

Hence, the radius of the circle is \(3\space cm\).

Question 7: Two concentric circles are of radii \(5\space cm\) and \(3\space cm\). Find the length of the chord of the larger circle which touches the smaller circle.

Answer:

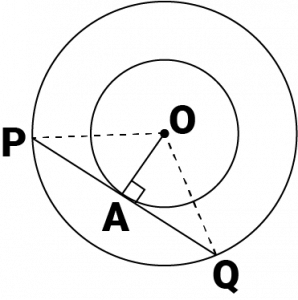
Let the two concentric circles be centered at point \(O\). And let \(PQ\) be the chord of the larger circle which touches the smaller circle at point \(A\). Therefore, \(PQ\) is tangent to the smaller circle.

\(OA ⊥ PQ\) (As \(OA\) is the radius of the circle)

Applying Pythagoras theorem in \(ΔOAP\), we obtain \(OA^2 + AP^2 = OP^2\)

\(3^2 + AP^2 = 5^2\)
\(9 + AP^2 = 25\)
\(AP^2 = 16\)

\(AP = 4\)

In \(ΔOPQ\),

Since \(OA ⊥ PQ\),

\(AP = AQ\) (Perpendicular from the center of the circle bisects the chord)
\(PQ = 2AP = 2 × 4 = 8\)

Therefore, the length of the chord of the larger circle is \(8\space cm\).

Question 8: A quadrilateral \(ABCD\) is drawn to circumscribe a circle (see given figure)

Prove that \(AB + CD = AD + BC\)

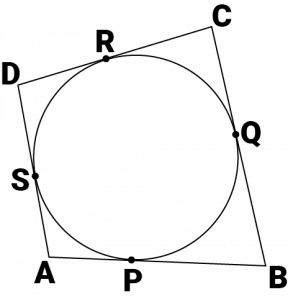
Answer:

It can be observed that

\(DR = DS\) (Tangents on the circle from point \(D\)) … (1)

\(CR = CQ\) (Tangents on the circle from point \(C\)) … (2)

\(BP = BQ\) (Tangents on the circle from point \(B\)) … (3)

\(AP = AS\) (Tangents on the circle from point \(A\)) … (4)

Adding all these equations, we obtain

\(DR + CR + BP + AP = DS + CQ + BQ + AS\)

\((DR + CR) + (BP + AP) \)

\(= (DS + AS) + (CQ + BQ) CD + AB \)

\(= AD + BC\)

Question 9: In the given figure, \(XY\) and \(X’Y’\) are two parallel tangents to a circle with centre \(O\) and another tangent \(AB\) with point of contact \(C\) intersecting \(XY\) at \(A\) and \(X’Y’\) at \(B\). Prove that

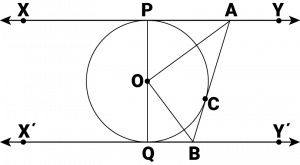
Answer: 

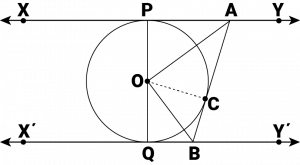
Answer:

Let us join point \(O\) to \(C\).

In \(ΔOPA\) and \(ΔOCA\),

\(OP = OC\) (Radii of the same circle)
\(AP = AC\) (Tangents from point \(A\))
\(AO = AO\) (Common side)

\(ΔOPA\)  and \(ΔOCA\) (SSS congruence criterion)
Therefore, \(P ↔ C, A ↔ A, O ↔ O\)
\(∠POA = ∠COA\)  … (i)

Similarly, \(ΔOQB\) and \(ΔOCB\)
\(∠QOB = ∠COB\) … (ii)

Since \(POQ\) is a diameter of the circle, it is a straight line.

Therefore, \(∠POA + ∠COA + ∠COB + ∠QOB = 180^0\)

From equations (i) and (ii), it can be observed that

\(2∠COA + 2 ∠COB = 180^0\)

\(∠COA + ∠COB = 90^0\) 
\(∠AOB = 90^0\)

Question 10: Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line-segment joining the points of contact at the centre.

Answer: 

Let us consider a circle centered at point \(O\). Let \(P\) be an external point from which two tangents \(PA\) and \(PB\) are drawn to the circle which are touching the circle at point \(A\) and \(B\) respectively and \(AB\) is the line segment, joining point of contacts \(A\) and \(B\) together such that it subtends \(∠AOB\) at center \(O\) of the circle.

It can be observed that

\(OA\) (radius) \(⊥ PA\) (tangent)
Therefore, \(∠OAP = 90^0\)

Similarly, \(OB\) (radius) \(⊥ PB\) (tangent)
\(∠OBP = 90^0\)

In quadrilateral \(OAPB\),

Sum of all interior angles \(= 360^0\)

\(∠OAP +∠APB+∠PBO +∠BOA = 360^0\) 
\(90^0 + ∠APB + 90^0 + ∠BOA = 360^0\)
\(∠APB + ∠BOA = 180^0\)

Hence, it can be observed that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line-segment joining the points of contact at the centre.

Question 11: Prove that the parallelogram circumscribing a circle is a rhombus.

Answer:

Since \(ABCD\) is a parallelogram,
\(AB = CD\) …(1)

\(BC = AD\) …(2)

It can be observed that

\(DR = DS\) (Tangents on the circle from point \(D\))
\(CR  = CQ\) (Tangents on the circle from point \(C\))
\(BP  = BQ\)  (Tangents on the circle from point \(B\))
\(AP  = AS\)  (Tangents on the circle from point \(A\))
Adding all these equations, we obtain
\(DR + CR + BP + AP = DS + CQ + BQ + AS\)
\((DR + CR) + (BP + AP) = (DS + AS) + (CQ + BQ)\)
\(CD + AB = AD + BC\)

On putting the values of equations (1) and (2) in this equation, we obtain

\(2AB = 2BC\)

\(AB = BC\) …(3)

Comparing equations (1), (2), and (3), we obtain

\(AB = BC = CD = DA\)

Hence, \(ABCD\) is a rhombus.

Question 12: A triangle \(ABC\) is drawn to circumscribe a circle of radius \(4\space cm\) such that the segments \(Bd\) and \(DC\) into which \(BC\) is divided by the point of contact \(D\) are of lengths \(8\space cm\) and \(6\space cm\) respectively (see given figure). Find the sides \(AB\) and \(AC\).

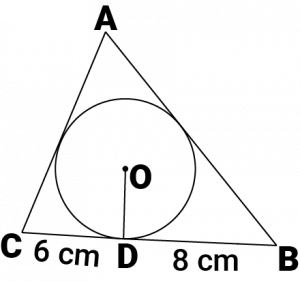
Answer: 

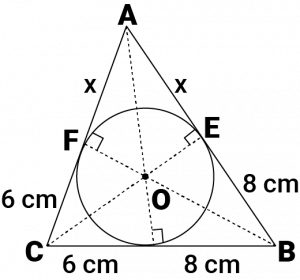
Let the given circle touch the sides \(AB\) and \(AC\) of the triangle at point \(E\) and \(F\) respectively and the length of the line segment \(AF\) be \(x\).

In \(ABC\),

\(CF = CD = 6\space cm\) (Tangents on the circle from point \(C\)) \(BE = BD = 8\space cm\) (Tangents on the circle from point \(B\)) \(AE = AF = x\) (Tangents on the circle from point \(A\)) \(AB = AE + EB = x + 8\)

\(BC = BD + DC = 8 + 6 = 14\)
\(CA = CF + FA = 6 + x\)
\(2s = AB + BC + CA\)
\(= x + 8 + 14 + 6 + x\)
\(= 28 + 2x\)

\(s = 14 + x\)

Area of \(\Delta ABC=\sqrt{s(s-a)(s-b)(s-c)}\)
\(=\sqrt{\lbrace14+x\rbrace(14+x)-14\lbrace(14+x)-(6-x)\rbrace\lbrace(14+x)(8+x)\rbrace}\)
\(\sqrt{(14+x)(x)(8)(6)}\)
\(=4\sqrt{3(14x+x^2)}\)
Area of \(\Delta OBC=\frac{1}{2}\times OF\times BC\)
\(=\frac{1}{2}\times4\times14=28\)
Area of \(\Delta OCA=\frac{1}{2}\times OD\times BC\)
\(=\frac{1}{2}\times4\times(6+x)=12+2x\)
Area of \(\Delta OAB=\frac{1}{2}\times OE\times AB\)
\(=\frac{1}{2}\times4\times(8+x)=16+2x\)
Area of \(\Delta ABC=\) Area of \(\Delta OBC+\) Area of \(\Delta OCA+\) Area of \(\Delta OAB\)
\(4\sqrt{3(14x+x^2)}=28+12+2x+16+2x\)
\(⇒4\sqrt{3(14x+x^2)}=56+4x\)
\(⇒\sqrt{3(14x+x^2 )}=14+x\)
\(⇒3(14x+x^2 )=(14+x)^2\)
\(⇒42x+3x^2=196+x^2+28x\)
\(⇒2x^2+14x-196=0\)
\(⇒x^2+7x-98=0\)
\(⇒x^2+14x-7x-98=0\)
\(⇒x(x+14)-7(x+14)=0\)
\(⇒(x+14)(x-7)=0\)
Either \(x+14 = 0\) or \(x − 7 =0 \)
Therefore, \(x = −14\) and \(7\)
However, \(x = −14\) is not possible as the length of the sides will be negative.
Therefore, \(x = 7 \)
Hence, \(AB = x + 8 = 7 + 8 = 15\space cm \)
\(CA = 6 + x = 6 + 7 = 13\space cm \)

Question 13: Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.

Answer:

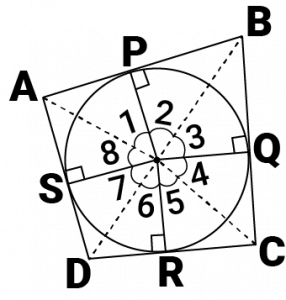
Let \(ABCD\) be a quadrilateral circumscribing a circle centered at \(O\) such that it touches the circle at point \(P, Q, R, S\).

Let us join the vertices of the quadrilateral \(ABCD\) to the center of the circle.

Consider \(ΔOAP\) and \(ΔOAS\),

\(AP = AS\) (Tangents from the same point)
\(OP = OS\) (Radii of the same circle)
\(OA = OA\) (Common side)

\(ΔOAP ≅ ΔOAS\) (SSS congruence criterion)
Therefore, \(A ↔ A, P ↔ S, O ↔ O\)
And thus, \(∠POA = ∠AOS\)
\(∠1 = ∠8\)

Similarly,
\(∠2 = ∠3\)
\(∠4 = ∠5\)
\(∠6 = ∠7\)

\(1 +  2 +  3 +  4 +  5 +  6 +  7 +  8 = 360^0\)

\(( 1 +  8) + ( 2 +  3) + ( 4 +  5) + ( 6 +  7) = 360^0\)

\(2 1 + 2 2 + 2 5 + 2 6 = 360^0\)

\(2( 1 +  2) + 2( 5 +  6) = 360^0\)

\(( 1 +  2) + ( 5 +  6) = 180^0\)

\(AOB +  COD = 180^0\)

Similarly, we can prove that  \(BOC +  DOA = 180^0\)

Hence, opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle