NCERT Solutions for Maths Class 10 Chapter 2

Exercise 2.1

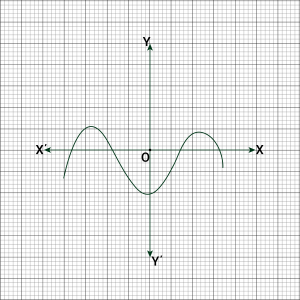
Question 1: The graphs of \(y = p(x)\) are given in following figure, for some polynomials \(p(x)\). Find the number of zeroes of \(p(x)\), in each case.

(i)

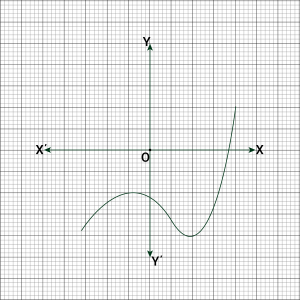
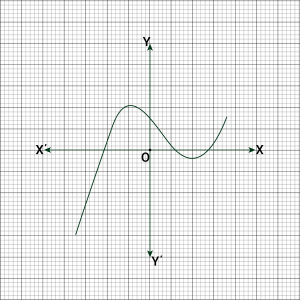
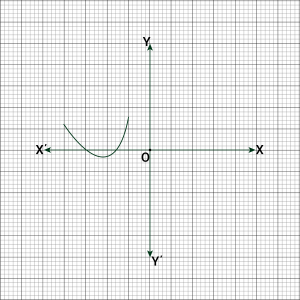
Answer: 

(i) The number of zeroes is \(0\) as the graph does not cut the \(x\)-axis at any point.

(ii) The number of zeroes is \(1\) as the graph intersects the \(x\)-axis at only \(1\) point.

(iii) The number of zeroes is \(3\) as the graph intersects the \(x\)-axis at \(3\).

(iv) The number of zeroes is \(2\) as the graph intersects the \(x\)-axis at \(2\) points.

(v) The number of zeroes is \(4\) as the graph intersects the \(x\)-axis at \(4\) points.

(vi) The number of zeroes is \(3\) as the graph intersects the \(x\)-axis at \(3\) points.

Exercise 2.2

Q.1: Find the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients.

(i) \(x^2-2x-8\)

(ii) \(4s^2-4s+1\)

(iii) \(6x^2-3-7x\)

(iv) \(4u^2+8u\)

(v) \(t^2-15\)

(vi) \(3x^2-x-4\)

Answer: 

(i) \(x^2-2x-8=(x-4)(x+2)\)

The value of \(x^2-2x-8\) is zero when \(x-4=0\) or \(x+2=0\), i.e., when \(x=4\) or \(x=-2\)

Therfore, the zeroes of \(x^2-2x-8\) are \(4\) and \(-2\).

Sum of zeroes \(4-2=\frac{-(-2)}{1}\)

\(=\frac{-(Coefficient\space of\space x)}{coefficient\space of\space x^2}\)

Product if zeroes \(=4\times(-2)=-8=\frac{-8}{1}\)

\(=\frac{Constant\space term}{Coefficient\space of\space x^2}\)

(ii) \(4s^2-4s+1=(2s-1)^2\)

The value of \(4s^2-4s+1\) is zero when \(2s-1=0\). i.e.s\(=\frac{1}{2}\)

Therefore, the zeroes of \(4s^2-4s+1\) are \(\frac{1}{2}\) and \(\frac{1}{2}\).

Sum of zeroes \(=\frac{1}{2}+\frac{1}{2}=1=\frac{-(-4)}{4}\)

\(=\frac{-(coefficient\space of\space s)}{coefficient\space of\space s^2}\)

(iii) \(6x^2-3-7x\) \(=6x^2-7x-3\) \(=(3x+1)(2x-3)\)

The value of \(6x^2-3-7x\) is zero when \(3x+1=0\) or \(2x-3=0\), i.e.,

\(x=-\frac{1}{3}\)  or \(x=\frac{3}{2}\)

Therfore, the zerose of \(6x^2-3-7x\) are \(-\frac{1}{3}\) and \(\frac{3}{2}\)

Sum of zeroes \(=-\frac{1}{3}+\frac{3}{2}=\frac{7}{6}=\frac{-(-7)}{6}\)

\(=\frac{-(coefficient\space of \space x)}{coefficient\space of\space x^2}\)

Product of zeroes \(=\frac{-1}{3}\times\frac{3}{2}=\frac{-1}{2}=\frac{-3}{6}\)

\(=\frac{constant\space term}{coefficient\space of \space y^2}\)

(iv) \(4u^2+8u=4u^2+8u+0\)

                \(=4u (u+2)\)

The value of \(4u^2+8u\) is zero when \(4u=0\) or \(u+2=0\), i.e., \(u=0\) or \(u=-2\)

Therefore, the zeroes of \(4u^2+8u\) are \(0\) and \(-2\).

Sum of zeroes \(=0+(-2)=-2=\frac{-(8)}{4}\)

\(=\frac{-(coefficient\space of\space u)}{coefficent\space of\space u^2}\)

Product of zeroes \(=0\times(-2)=0=\frac{0}{4}\)

\(=\frac{constant\space term}{coefficient\space of\space u^2}\)

(v) \(t^2-15\)

\(=t^2-0_1-15\)

\(=(t-\sqrt{15})(t=\sqrt{15})\)

The value of \(t^2-15\) is zero when \(t-\sqrt{15}=0\) or \(t+\sqrt{15}=0\),

i.e., when \(t=\sqrt{15}\) or \(t=-\sqrt{15}=0\)

Therefore, the zeroes of \(t^2-15\) are \(\sqrt{15}\) and \(-\sqrt{15}\)

Sum of zeroes \(=\sqrt{15}+(-\sqrt{15})=0=\frac{-0}{1}\)

\(=\frac{-(coeffocoent\space of\space t)}{coefficient\space of\space t^2}\)

Product of zeroes \(=(\sqrt{15})(-\sqrt{15})=-15=-\frac{15}{1}\)

\(=\frac{constant\space term}{coefficient\space of \space x^2}\)

(vi) \(x^2-x-4\)

\(=(3x-4)(x+1)\)

The value of \(3x^2-x-4\) is zero when \(3x-4=0\) or \(x+1=0\), i.e.

When \(x=\frac{4}{3}\) or \(x=-1\)

Therefore, the zeroes of \(3x^2-x-4\) are \(\frac{4}{3}\) and \(-1\).

Sum of zeroes=Product of zeroes

Q.2: Find a quadratic polynomial each with the given numbers as the sum and product of its zeroes respectively.

(i) \(\frac{1}{4},1\)      (ii) \(\sqrt2,\frac{1}{2}\)      (iii) \(0,\space\sqrt5\)

(iv) \(1,\space1\)      (v) \(-\frac{1}{4}m\frac{1}{4}\)     (vi)  \(4,\space1\)

Answer:

(i) \(\frac{1}{4},1\)

Let the polynomial be \(ax^2+bx+c\) and its zeroes be \(\alpha\) and \(\beta\)

\(\alpha+\beta=\frac{1}{4}=-\frac{b}{1}\)

\(\alpha\beta=-1=-\frac{4}{4}=\frac{c}{a}\)

If \(a=4\), then \(b=-1,\space c=-4\)

Therefore, the quadratic polynomial is \(4x^2-x-4\)

(ii) \(\sqrt2, \frac{1}{3}\)

Let the polynomial be \(ax^2+bx+c\) and its zeroes be \(\alpha\) and \(\beta\).

\(\alpha+\beta=\sqrt2=\frac{3\sqrt2}{3}=-\frac{b}{a}\)

\(\alpha\beta=\frac{1}{3}=\frac{c}{a}\)

If \(a=3\), then \(b=-3\sqrt2,\space c=1\)

Therefore, the quadratic polynomial is \(3x^2-3\sqrt2x+1\).

(iii) \(0,\space\sqrt5\)

Let the polynomial be \(ax^2+bx+c\) and its zeroes be \(\alpha\) and \(\beta\).

\(\alpha+\beta=0=\frac{0}{1}=-\frac{b}{a}\)

\(\alpha\times\beta\sqrt5=\frac{\sqrt5}{1}=\frac{c}{a}\)

If \(a=1\), then \(b=0,\space c=\sqrt5\)

Therefore, the quadratoc polynomial is \(x^2+\sqrt5\)

(iv) \(1,\space1\)

Le the polynomial be \(ax^2+bx+c\) and its zeroes be \(\alpha\) and \(\beta\).

\(\alpha\beta=1=\frac{1}{1}=-\frac{b}{a}\)

\(\alpha\times\beta=1=\frac{1}{1}=\frac{c}{a}\)

If \(a=1\), then \(b=1,\space c=1\)

Therefore, the polynomial quadratic polynomial is \(x^2-x+1\)

(v) \(-\frac{1}{4},\frac{1}{4}\)

Let the polynomial be \(ax^2+bx+c\) and its zeroes be \(\alpha\) and \(\beta\).

\(\alpha+\beta=-\frac{1}{4}=-\frac{b}{a}\)

\(\alpha\times\beta=\frac{1}{4}=\frac{c}{a}\)

If \(a=4\), then \(b=1,\space c=1\)

Therefore, the quadratic polynomial is \(4x^2+x+1\).

(vi) \(4,\space1\)

Let the polynomal be \(ax^2+bx+c\).

\(\alpha+\beta=4=\frac{4}{1}=-\frac{b}{a}\)

\(\alpha\times\beta=1=\frac{1}{2}=\frac{c}{a}\)

If \(a=1\), then \(b=-4,\space c=1\)

Therefore, the quadratic polynomial is \(x^2-4x+1\)

Q.2: Check whether the first polynomial is a factor of the second polynomial by dividing the second polynomial by the first polynomial:

(i) \(t^2-3,\space 2t^4+3t^3-2t^2-9t-12\)

(ii) \(x^2+3x+1,\space 3x^4+5x^3-7x^2+2x+2\)

(iii) \(x^3-3x+1,\space x^5-4x^3+x^2+3x+1\)

Answer: 

(i) \(t^2-3,\space 2t^4+3t^3-2t^2-9t-12\)

\(t^2-3=t^2 0t-3\)

Since the remainder is \(0\),

Hence, \(t^2-3\) is a factor of \(2t^4+3t^3-2t^2-9t-12\)

(ii)

Since the remainder is \(0\),

Hence, \(x^2+3x+1\) is a factor of \(3x^4+5x^3-7x^2+2x+2\)

(iii) 

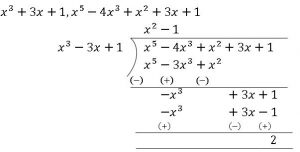
Since the remainder \(≠0\),

Hence, \(x^3-3x+1\) is not a factor of \(x^5-4x^3+x^2+3x+1\)

Q.3: Obtain all other zeroes of \(3x^4+6x^3-2x^2-10x-5\), if two of its zeroes are \(\sqrt{\frac{5}{3}}\) and \(-\sqrt{\frac{5}{3}}\)

Answer:

\((p)x=3x^4+6x^3-2x^2-10x-5\)

Since the two zeroes are \(\sqrt{\frac{5}{3}}\) and \(-\sqrt{\frac{5}{3}}\)

\( ∴(x-\sqrt{\frac{5}{3}})(x+\sqrt{\frac{5}{3}})=(x^2-\frac{5}{3})\) is a factor of \(3x^2+6x^2-2x^2-10x-5\)

Therefore, we divide the given polynomial by \(x^2-\frac{5}{3}\)

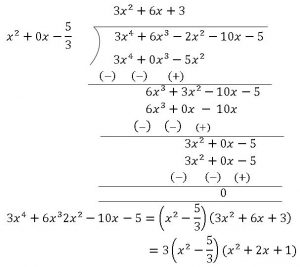
\(3x^4+6x^3 2x^2-10x-5\) \(=(x^2-\frac{5}{3})(3x^2+6x+3)\) 

\(=3(x^2-\frac{5}{3})(x^2+2x+1)\)

We factorize \(x^2+2x+1\)

                        \(=(x+1)^2\)

Therefore, its zero is given \(by x+1=0\)

As it has the term \((x+1)^2\), therefore, there will be \(2\) zeroes at \(x=-1\)

Hence, the zeroes of the given polynomial are \(\sqrt{\frac{5}{3}},-\sqrt{\frac{5}{3}},-1\) and \(-1\).

Q.4: On dividing \(x^3-3x^2+x+2\) by a polynomial \(g(x)\), the quotient and remainder were \(x – 2\) and \(- 2x + 4\), respectively. Find \(g(x).\)

Answer:

\((x)=x^3-3x^2+x+2\) (Divided)

\(g(x) = ?\) (Divisor)

Quotient \(= (x − 2)\)

Remainder \(= (− 2x + 4)\)

Dividend = Divisor × Quotient + Remainder

\(x^3-3x^2+x+2\)

\(=g(x)×(x-2)+(-2x+4)\)

\(x^3-3x^2+x+2+2x-4\)

\(=g(x)(x-2)\)

\(x^3-3x^2+3x-2\)

\(=g(x)(x-2)\)

\(g(x)\) is the quotient when we divide \((x^3-3x^2+3x-2)\) by \((x-2)\)

Q.5: Give examples of polynomial \(p(x),\space g(x),\space q(x)\) and \(r(x)\), which satisfy the division algorithm and

(i)  \(deg p(x) = deg q(x)\)
(ii) \(deg q(x) = deg r(x)\)
(iii) \(deg r(x) = 0\)

Answer: According to the division algorithm, if \(p(x)\) and \(g(x)\) are two polynomials with \(g(x) ≠0\), then we can find polynomials \(q(x) \) and \(r(x)\) such that \(p(x) = g(x) × q(x) + r(x)\), where \(r(x) =0\) or degree of \(r(x) <\) degree of \(g(x)\)

Degree of a polynomial is the highest power of the variable in the polynomial.

(i) deg \(p(x) =\) deg \(q(x)\)

Degree of quotient will be equal to degree of dividend when divisor is constant ( i.e., when any polynomial is divided by a constant).

Let us assume the division of \(6x^2+2x+2\) by \(2\).

Here, \(p(x) =\)
\(g(x) = 2\)

\(q(x) =3x^2+x+1\) and \(r(x) = 0\)

Degree of \(p(x)\) and \(q(x)\) is the same i.e., \(2\)

Checking for division algorithm,

\(p(x) = g(x) × q(x) + r(x)\)

\(=2\)

\(=6x^2+2x+2\)

Thus, the division algorithm is satisfied.

(ii) deg \(q(x) =\) deg \(r(x)\)

Let us assume the division of \(x^3 + x\) by \(x^2\),

Here, \(p(x) = x^3 + x\)

\(g(x) = x^2\)

\(q(x) = x\) and \(r(x) = x\)

Clearly, the degree of \(q(x)\) and \(r(x)\) is the same i.e., \(1\)

Checking for division algorithm,

\(p(x) = g(x) × q(x) + r(x)\)
\(x^3 + x = (x^2 ) × x + x\)
\(x^3 + x = x^3 + x\)

Thus, the division algorithm is satisfied.

(iii) deg \(r(x) = 0\)

Degree of remainder will be \(0\) when remainder comes to a constant.

Let us assume the division of \(x^3 + 1\) by \(x^2\).

Here, \(p(x) = x^3 + 1\)

\(g(x) = x^2\)

\(q(x) = x\) and \(r(x) = 1\)

Clearly, the degree of \(r(x)\) is \(0\). Checking for division algorithm, \(p(x) = g(x) × q(x) + r(x)\)
\(x^3 + 1 = (x^2 ) × x + 1\)
\(x^3 + 1 = x^3 + 1\)

Thus, the division algorithm is satisfied.

Exercise 2.4

Q.1: Verify that the numbers given alongside of the cubic polynomials below are their zeroes. Also verify the relationship between the zeroes and the coefficients in each case:

(i) \(2x^3+x^2-5x+2;\frac{1}{2}, 1, -2\)

(ii) \(x^3-4x^2=5x-2;2, 1,1\)

Answer:

(i) \(p(x)=2x^3+x^2-5x+2.\)

Zeroes fro this polynomual are \(\frac{1}{2},\space 1,\space -2\)

\(p(\frac{1}{2})=2(\frac{1}{2})^3+(\frac{1}{2})^2-5(\frac{1}{2})+2\)

\(=\frac{1}{4}+\frac{1}{4}-\frac{5}{2}+2\)

\(=0\)

\(p(1)=2×1^3+1^2-5×1+2\)

\(=0\)

\(p(-2)=2(-2)^3+(-2)^2-5(-2)+2\)

\(=-16+4+4+10+2=0\)

Therefore \(\frac{1}{2},\space 1,\) and \(-2\) are the zeroes of the given polynomial.

Comparing the given polynomial with \(ax^3+bx^2+cx+d\), we obtain

\(a=2,\space b=1,\space c=-5,\space d=2\)

We can take \(α=\frac{1}{2},\space β=1,\space y=-2\)

\(α+β+γ+\frac{1}{2}+1+(-2)\) \(=-\frac{1}{2}=-\frac{b}{a}\)

\(αβ+βγ+αγ=\frac{1}{2}×+1(-2)+\frac{1}{2}(-2)\) \(=-\frac{5}{2}=\frac{c}{a}\)

\(αβγ=\frac{1}{2}×1×(-2)=-\frac{1}{1}\) \(=\frac{-(2)}{2}=-\frac{d}{a}\)

Therefore, the relationship between the zeroes and the coefficients is verified.

(ii) \(p(x)=x^3-4x^2+5x-2\)

Zeroes for this polynomial are \(2, 1,  1.\)

\(p(2)=2^3-4(2^2 )=5(2)-2\)

\(=8-16+10-2=0\)

\(p(1)=1^3-4(1)^2+5(1)-2\)

\(=1-4+5-2=0\)

Therefore, \(2,\space 1,\space 1\) are the zeroes of the given polynomial.

Comparing the given polynomial with \(ax^3 0+bx^2+cx+d\),

we obtain \(a = 1,\space b = −4,\space c = 5,\space d = −2\)

Verification of the relationship between zeroes and coefficient of the given Polynomial

Sum of zeroes \(=2+1+1=4=\frac{(-4)}{1}=-\frac{b}{a}\)

Multiplication of zeroes taking two at a time \(= (2)(1) + (1)(1) + (2)(1)\)

\(=2+1+2=5=\frac{(5)}{1}=\frac{c}{a}\)

Multiplication of zeroes \(=2×1×1=2=\frac{-(-2)}{1}=-\frac{d}{a}\)

Hence, the relationship between the zeroes and the coefficients is verified.

Q.2: Find a cubic polynomial with the sum, sum of the product of its zeroes taken two at a time, and the product of its zeroes as \(2,\space − 7,\space − 14\) respectively.

Answer:

Let the polynomial be \(ax^3+bx^2+cx+d\) and the zeroes be \(α, β\) and \(γ\).

It is given that

\(α+β+γ=\frac{2}{1}=-\frac{b}{a}\)

\(αβ+βγ+αγ=-\frac{7}{1}=\frac{c}{a}\)

\(αβγ=-\frac{14}{1}=-\frac{d}{a}\)

If \(a = 1\), then \(b = -2,\space c = -7,\space d = 14\)

Hence, the polynomial is \(x^3-2x^2-7x+14\)

Coerrect: \(x^3-2x^2-7x+14\)

Q.3: If the zeroes of polynomial  are , find |(a\) and \(b\).

Answer:\(p(x)=x^3-3x^2+x+1\)

Zeroes are \(a − b,\space a + a + b\)

Comparing the given polynomial with \(px^3+qx^2 rx+t\), we obtain

\(p = 1,\space q = −3,\space r = 1,\space t = 1\)

Sum of zeroes\(=a-b+a+a+b\)

\(\frac{-q}{p}=3a\)

\(\frac{-(-3)}{1}=3a\)

\(3=3a\)

\(a=1\)

The zeroes are \(1-b,\space 1,\space 1+b\)

Multiplication of zeroes \(=1(1-b)(1+b)\)

\(\frac{-t}{p}=1-b^2\)

\(\frac{-1}{1}=1-b^2\)

\(l-b^2=-1\)

\(1+1=b^2\)

\(b+±\sqrt2\)

Hence, \(a=1\) and \(b=\sqrt2\)  or \(-\sqrt2\)

Q.4: It two zeroes of the polynomial \(x^4-6x^3-26x^2+138x-35\) are \(2±\sqrt3\) find other zeroes.

Answer: Given that \(2+\sqrt3\)  and \(2-\sqrt3\)  are zeroes of the given polynomial.

Therefore, \((x-2-\sqrt3)(x-2+\sqrt3)\) \(=x^2+4-4x-3\)

\(=x^2-4x+1\) is a factor of the given polynomial

For finding the remaining zeroes of the given polynomial, we will find the quotient by dividing \(x^4-6x^3-26x^2+138x-35\) by \(x^2 4x+1\)

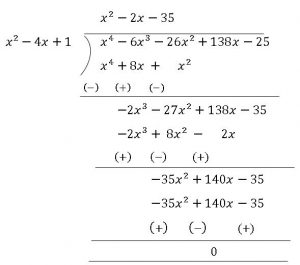
Clearly, \(x^4-6x^3-26x^2+138x-35\) \(=(x^2-4x+1)(x^2-2x-35)\)

It can be observed that \((x^2-2x-35)\) is also a factor of the given polynomial.

And \((x^2-2x-35)=(x-7(x+5)\)

Therefore, the value of the polynomial is also zero when \(x-7=0\) or \(x+5=0\)

Or \(x=7 or -5\)

Hence, \(7\) and \(-5\) are also zeroes of this polynomial.

Or \(x = 7\) or \(-5\)

Hence, \(7\) and \(-5\) are also zeroes of this polynomial.

Q.5: If the polynomial \(x^4-6x^3+16x^2-25x+10\) is divided by another polynomial \(x^2-2x+k\), the remainder comes out to be \(x + a\), find \(k\) and \(a\).

Answer:

By division algorithm,

Dividend = Divisor × Quotient + Remainder
Dividend – Remainder = Divisor × Quotient

\(x^4-6x^3+16x^2-25x+10-x-1\) \(=x^4-6x^3+16x^2-26x+10-a\)

will be perfectly divisible by \(x^2-2x+k\)

Let us divide by

\(x^4-6x^3+16x^2-26x+10-a\) by \(x^2-2x+k\)

It can be observed that \((-10+2k)x+(10-1-8k+k^2)\) will be \(0\).

Therefore, \((-10+2k)=0\) and \((10-a-8k+k^2 )=0\)

For \((-10+2k)=0\)

\(2 k=10\)

And thus, \(k=5\)

For \((10-a-8k=k^2 )=0\)

\(\Rightarrow10-a-8×5+25=0\)

\(\Rightarrow10-a-40+25=0\)

\(\Rightarrow-5-a=0 \)

Therefore, \(a=-5\)

Hence, \(k=5\) and \(a=-5\)