NCERT Solutions for Science Class 9 Chapter 7

Chapter 7: Motion

Question 1: An object has moved through a distance. Can it have zero displacement? If yes, support your answer with an example.
Answer: Yes. An object can have zero displacement if it has moved through a distance.
Displacement is defined as the shortest distance from the initial point to the final point.
Hence, if the starting (initial) point is the same as the final point then the displacement of the object is zero.
Suppose a man is walking in a square park of length 20m. He starts from point A and walks along all the corners of the park through points B, C and D and comes back to the same point A.
The total distance covered by the man $20m+20m+20m+20m=80m$.
As the starting point and final point are same, the shortest distance between his initial and final position is zero
Therefore, the displacement is zero.
Question 2: A farmer moves along the boundary of a square field of side 10m in 40s .What will be the magnitude of displacement of the farmer at the end of 2 minutes 20 seconds?
Answer: It is given that,

Farmer takes 40 s to cover a square field of side 10 m.

$⇒Distance=4\times10=40\space m$

It is known that, $Spee=\frac{Distance}{Time}$

$⇒Speed=\frac{40}{40}=1$

Therefore, speed of the farmer is $1\space m/s$.

In 2 minutes 20 seconds distance travelled is $Speed\times Time$.

$⇒Distance=1\times(2\times60+20)$

$⇒Disatance =140\space m$

Number of rounds farmer covered $=\frac{140}{40}=3.5$

After 2 minutes 20 seconds the farmer will be at the opposite end of starting point, completing 3 and half rounds.

1. If the farmer starts from any corner of the field: The displacement will be equal to the diagonal of the field.

$⇒Displacement=\sqrt{10^2+10^2}=14.14\space m$

Question 2: If the farmer starts from the middle point of any side of the field: The final point will be the middle point of the side opposite to the initial point.

$⇒Displacement=10\space m$

Therefore, the magnitude of displacement if the farmer starts at any corner is 14.14 m and if the farmer statrs from middle point of any side is 10 m.

Question 3: Which of the following is true for displacement?
1. It cannot be zero.
Answer: Not true. When the initial and final position of the object is the same, then the displacement is zero.

2. Its magnitude is greater than the distance travelled by the object.
Answer: Not true. Displacement is the measure of the shortest distance between the initial and final position of an object.
Therefore, it is always smaller than or equal to the magnitude of distance travelled by the object.

Question 4: An artificial satellite is moving in a circular orbit of radius 42250km. Calculate its speed if it takes 24 hours to revolve around the earth?
Answer: It is given that,
Radius of the circular orbit,

$r=42250\space km$

Time taken by the satellite to revolve around earth, $t=24\space h$

Speed of the artificial satellite, $v=?$

It is known that,

$v=\frac{2\pi r}{t}$

$⇒v=\frac{2\times3.14\times42250}{24}$

$⇒v=1.105\times10^4\space km/h$

$⇒v=\frac{1.105\times10^4}{3600}\space km/s$\

$⇒v=3.069\space km/s$

Therefore, the speed of the artificial satellite is $v=3.069\space km/s$.

Question: Distinguish between speed and velocity.
Answer: The differences between speed and velocity are as follows:

Question 6: Under what condition(s) is the magnitude of average velocity of an object added equal to its average speed?

Answer: It is known that

Average speed $=\frac{Total\space distance\space covered}{Total\space time\space taken}$

Therefore, the magnitude of average velocity of an object is equal to its average speed when total distance covered is equal to the displacement.
Question 7: What does the odometer of an automobile measure?
Answer: The distance covered by an automobile is recorded by the odometer of an automobile.

Question 8: What does the path of an object look like when it is in uniform motion?
Answer: An object has a straight-line path when it is in uniform motion.
Question 9: During an experiment, a signal from a spaceship reached the ground station in five minutes. What was the distance of the spaceship from the ground station? The signal travels at the speed of light, that is, $3\times10^8ms^{-1}$

Answer: It is given that,

Time taken by a signal to reach ground from a spaceship $=5\space min=5\times60=300\space sec$

Speed of the signal is equal to speed of light

$=3\times10^8ms^{-1}$

It is known that,

$Speed=\frac{Distance\space travelled}{Time\space taken}$

$⇒Distance\space travelled=Speed\times Time\space taken$

$⇒Distance\space travelled=3\times10^8\times300=9\times10^{10}m$

Therefore, the distance of the spaceship from the ground station is $9\times10^{10}m$.

Question 10: When will you say a body is in
1. uniform acceleration?
Answer: When the magnitude and the direction of acceleration of a body is constant i.e., velocity changes at an equal rate then the body is said to be in uniform acceleration.

2. non-uniform acceleration?
Answer: When the acceleration of a body changes in magnitude or direction or both i.e., velocity changes at an unequal rate then the body is said to be in non-uniform
acceleration.

Question 11: A bus decreases its speed from $80\space kmh^{-1}$ to $60\space kmh^{-1}$ in 5s. Find the acceleration of the bus.

Answer: It is given that,

Intial speed of the bus, $u=80\space km/h$

$⇒u=80\times\frac{5}{18}m/s=22.22\space m/s$

Final speed of the bus, $v=60\space km/h$

$⇒v=60\times\frac{5}{18}m/s=16.66\space m/s$

Time taken to decrease speed, $t=5s$

It is known that,

Acceleration, $a=\frac{v-u}{t}$

$⇒a=\frac{16.66-22.22}{5}$

$⇒a=-1.112\space m/s^2$

Therefore, the acceleration of the bus is $-1.112\space m/s^2$. The negative sign indicates that the velocity of the car is decreasing. Decreasing acceleration is called retardation.

Question 12: A train starting from a railway station and moving with uniform accelerationattains a speed 40 km/h in hin 10 minutes. Find its acceleration.

Answer: It is given that,

Intial velocity of the train, $u=0$  (The train is starting from rest)

Final velocity of the train, $v=40\space km/h$

$⇒v=40\times\frac{5}{18}mm/s=11.11\space m/s$

Time taken, $t=10\times60=600\space s$

It is known that,

Acceleration, $a=\frac{v-u}{t}$

$⇒a=\frac{11.11-0}{600}$

$⇒a=0.0185\space m/s^2$

Therefore, the acceleration of the train is $0.0185\space m/s^2$

Question 13: What is the nature of the distance-time graphs for uniform and non-uniform motion of an object?

Answer: The distance-time graph for uniform motion of an object is a straight line.

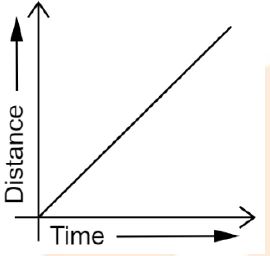
The distance-time graph for non-uniform motion of an object is a curved line.

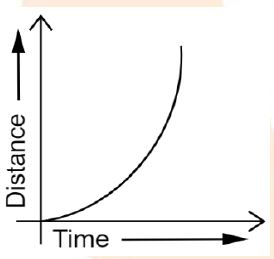
Question 14: What can you say about the motion of an object whose distance-time graph is a straight line parallel to the time axis?
Answer: A straight line parallel to the x-axis in a distance-time graph indicates that the position of the object does not change with time.

Therefore, the object is said to be at rest.

Question 15: What can you say about the motion of an object if its speed-time graph is a straight line parallel to the time axis?
Answer: A straight line parallel to the time axis in a speed-time graph indicates that the speed of the object does not change with time.

Therefore, the object is moving uniformly.

Question: What is the quantity which is measured by the area occupied below the velocitytime graph?
Answer: The area of the velocity-time graph is displacement.
Consider the following figure which shows the velocity-time graph of a uniformly moving body.

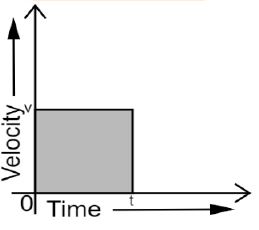
Let, the valocity of the body at time $t$ be $v$.

Where,

Length $=l$

Breadth $=v$

$⇒Area=vt=velocity\times time$ ….. (1)

It is known that,

$Velocity=frac{Displacement}{time}$

$⇒Displacement=Velocity\times Time$  …(2)

From equation (1) and (2)

$⇒Area = Displacement$

Hence, the area occupied below the velocity-time graph measures the displacement of the body.

Question 17: A bus starting from rest moves with a uniform aceleration of $0.1\space m/s^2$ for $2$ minutes. Find

1. The speed acquired

Answer: 

It is given that,

Intial velocity of the bus, $u=0$  (Bus is starting from rest)

Accekeration ofbus, $a=0.1\space m/s^2$

Time taken, $t=2\space min=120\space sec$

Final velocity of the bus, $v=?$

It is known that,

Acceleration, $a=\frac{v-u}{t}$

$⇒0.1=\frac{v-0}{120}$

$⇒v=12\space m/s$

Therefore, the speed acquired is $v=12\space m/s$

Question 2: The distance travelled

Answer: It is known that

From, third equation of motion: $v^2-u^2=2as$

$⇒(12)^2-(0)^2=2\times(0.1)\times s$

$⇒144=0.2\space s$

$⇒s=720\space m$

Therefore, the distance travelled is $s=720\space m$

Question 18: A train is travelling at a speed of $90\space kmh^{-1}$. Brakes are applied so as to produce a unifrom acceleration of $-0.5ms^{-1}$. Find how far the train will go before it is brought to rest.

Answer:

It is given that,

Intial speed of a train, $u=90\space km/h$

$⇒u=90\times\frac{5}{18}=25\space m/s$

Final speed of the train, $v=0$ (Train comes to rest finally

Accekeration of train, $a=-0.5\space m/s^2$

Distance covered by the train, $s=?$

It is known that,

From, third equation of motion: $v^2-u^2=2as$

$⇒(0)^2-(25)^2=2\times(-0.5)\times s$

$⇒-625=-s$

$⇒s=625\space m$

Therefore, the train covers a distance of $625\space m$ before it comes to rest.

Question 19: A trolley, while going down an incline plane, has an acceleration of $2\space cm/s^2$. What will be its velocity $3s$ after the start?

Answer: It is given that,

Intial velocity of the trolley, $u=0$ (Trolley is starting from rest)

Acceleration of the trolley, $a=2\space cm/s^2=0.02\space m/s^2$

Time taken, $t=3s$

Final velocity (after 3s of start) of ther trolley, $v=?$

It is known that,

From, first equation of motion: $v=u+at$

$⇒v=0+0.02(3)$

$⇒v=0.06\space m/s$

Thus, the velocity of the trolley is $0.06\space m/s$ after $3s$ from the start.

Question 20: A racing car has a uniform acceleration of $4\space ms^{-2}$. What distance will it cover in $10s$ after start?

Answer: It is given that,

Intial velocity of the racing car, $u=0$ (The racing car is initially at rest)

Acceleration of a racing car, $a=4m/s^2$

Time taken, $t=10s$

It is known that,

From, second equation of motion: $s=ut+\frac{1}{2}at^2$

$⇒s=0+\frac{1}{2}(4)(10)^2$

$⇒s=200\space m$

Therefore, the distance by racing car after $10\space s$ from start is $200\space m$.

Question 21: A stone is thrown in a vertically upward direction with a velocity of $5m/s$. If the acceleration of the stone during its motion is $10m/s^{-2}$ in the downward direction, what woll be theheight attained by the stone an how much time will it take to reach there?

Answer: It is given that,

Intial velocity of the stone, $u=5/s$

Final velocity, $v=0$ (Stone comes to rest after reaching maximum height)

Acceleration of the stone is equal to acceleration due to gravity, $a=-10,/s^2$ (Negative sign because of fownward direction)

Maximum height reached by the stone, $s=?$

It is known that,

From, first equation of motion: $v=u+at$

$⇒0=5+(-10)t$

$⇒5=10t$

$⇒t=0.5s$

From, third equation of motion: $v^2-u^2=2as$

$⇒(0)^2-(5)^2=2(-10)s$

$⇒-25=-20s$

$⇒s=1.25m$

Therefore, the height attained by the stone is $1.25,$ in $0.5s$.

Question 22: An athlete completes one round of a circular track of diameter 200m in 40s. What will be the distance covered and the displacement at the end of 2 minutes 20s?

Answer: It is given that,

Diameter of a circular track, $d=200m$

Radius of the circular track, $r=\frac{d}{2}$

$⇒r=\frac{200}{2}=100m$

Circumference of the circular track, $c=2\pi r$

$⇒c=2\pi(100)=200\pi m$

Time taken to cove one round, $t=40s$

It is known that,

$Speed=\frac{Distance\space travelled}{Time\space taken}$

$⇒Speed=\frac{200\pi}{40}$

$⇒Speed=50\space \pi$

Athelete runs for 2 minutes $$20$s$. Time in seconds $=120+20=140s$

Total distance covered in

$140s=Speed\times Time$

$⇒Distance=\frac{200\times22\times140}{40\times7}=2200m$

Number of rounds $=140\frac{140}{40}=3.5$

Athlete will be diametrically opposite to the point where he started after completing three
rounds.
The displacement will be equal to diameter i.e.,200m
Therefore, the distance covered is 2200 and the displacement is 200mat the end of 2 minutes
20s.
Question 23: Joseph jogs from one end A to the other end B of a straight road of 300m in 2 minutes 50 seconds and then turns around and jogs 100m back to point C in another 1 minute. What are Joseph’s average speeds and velocities in jogging

1. from A to B

Answer: it is given that,

Distance from A to B=30 m

Time taken from A to B

= 2 min 50 sec=170 sec

It is known that,

Average\space speed=\frac{Total\space distance\space covered}{Total\space time\space taken}\)

$⇒Average\space speed=\frac{300}{170}=1.75\space m/s$

Average\space velocity=\frac{Displacement}{Total\space time\space taken}\)

Displacement from A to B=Distance=300 m

$Average\space velocity=\frac{300}{170}=1.76\space m/s$

Therefore, the average speed an velocity of Joseph from A to B are same and is equal to 1.765 m/s.

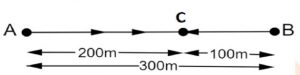
Question 2: From A to C?

Answer: It is given that,

Distance from A to B=300 m

Distance from B to C=100 m

Total distance A to C=300+100=400 m

Time taken from A to B = 2min 50 sec=170 sec

Time taken from B to C=1 min=60 sec

Total time taken from A to C=170=60=230 sec

It is known that

Average Speed $=\frac{Total\space distance\space covered}{Total\space time\space taken}$

$⇒Average\space speed=\frac{400}{230}=1.739\space m/s$

Average velocity $=\frac{Displacement}{Total\space time\space taken}$

Displacement from A to C = AB-BC=300-100=200 m

Average velocity $=\frac{200}{23)}=0.87\space m/s$

Therefore, the average speed and average velocity of Joseph from A to C are 1.739 m/s respectively.

Question 24: Abdul, while driving to school, computes the average speed for his trip to be $20\space kmh^{-1}$. On his return trip along the route, there is less traffic and the average speed $40\space kmh^{-1}$. What is the average speed for Abdul’s trip?

Answer: It is given that,

Average speed of Abdul’s trip $=20\space km/h$

Let the distance travelled by Abdul to reach school and to return home be $d$.

Case 1: While driving to school

Let, total time taken be $t_1$.

Average Speed=\frac{Total\space distance\space coveref}{Total\space time\space taken}\)

$⇒20=\frac{d}{t_1}$

$⇒t_1=\frac{d}{20}$     …(1)

Case 2: While returning from school

Let, total time taken be $t_2$.

Average speed $=\frac{Total\space distance\space covered}{Total\space time\space taken}$

$⇒4-=\frac{d}{t_2}$

$⇒t_2=\frac{d}{40}$   ….(2)

Average speed for Abdul’s trip $=Total\space distance\space covered\space in\space the\space trip}{Total\space time\space taken}$

Where,

Total distance covered in the trip $=d+d=2d$

Total time taken $=t_1+t_2$

Substitute equation (1) and (2) in total time takne

Total time takne $=\frac{d}{20}+\frac{d}{40}$

$⇒Average\space speed=\frac{2d}{\frac{d}{20}+\frac{d}{40}}$

$⇒Average\space speed=\frac{2}{\frac{2+1}{40}}=\frac{80}{3}$

$⇒Average\space speed=26,67\soace m/s$

Therefore, the average speed for Abdul’s trip is $26.67\space m/s$.

Question 25: A motorboat starting from rest on a lake accelerates in a straight line at a constant rate of $3.0\space m/s^2$ for $8.0\space s$. How far does the boat travel during this time?

Answer: It is given that,

The initial velocity of the motorboat, $u=0$ (Motortboar is nitially at rest)

Acceleration of the motorboat, $a=3\space m/s^2$

Time takne, $t=8\space s$

Distance travelled by the motorboat, $s=?$

From, second equation of motion: $s=ut+\frac{1}{2}at^2$

$⇒s=0+\frac{1}{2}(3)(8)^2$

$⇒s=(3)(8)(4)$

$⇒s=96\space m$

Therefore, the boat travels a distance of $96\space m$

Question 26: A driver of a car travelling at $52\space kmh^{-1}$ applies the brakes and accelerates uniformly in the opposite direction. The car stops in $5\space s$. Another driver going at $3\space kmh^{-1}$ in another car applies his brakes slowly and stops in $10\space s$. On the same graph paper, plot the speed versus time graphs for the two cars. Which of the two cars travelled farther after the brakes were applied?

Answer: Car A: Intial speed of the car,