NCERT Solutions for Maths Class 9 Chapter 9

CHAPTER 9

Exercise 9.1:

Question 1: Recall that two circles are congruent if they have the same radii. Prove that equal chords of congruent circles subtend equal angles at their centres. 

Answer: 

Given: Two given circles are congruent when they have the same radii.
To Prove: Equal chords of the congruent circles subtend equal angles at their centres.
A circle is a collection of equidistant points around a given point. This fixed location is known as the circle’s centre, and this equal distance is known as the circle’s radius. As a result, the radius of a circle determines its form. As a result, it can be seen that if two circles of equal radius are superimposed, both circles will cover each other. As a result, two circles are congruent if their radius is the same.

Consider two congruent circles having centre O and O’ and two chords AB and CD of equal lengths.

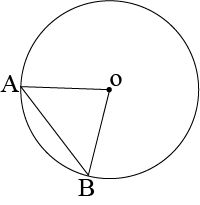
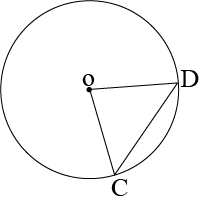
In $\triangle AOB$ and $\triangle COD$,

$AB=CD$ (Chords of sa,e length)

$OA=O’C$ (Radii of congruent circles)

$OB=OD$ (Radii of confruent circles)

$∴\triangle AOB≅\triangle CO’D$  (SAS comgruence rule)

$⇒\angle AOB=\angle COD$  (By CPCT)

Hence, equal chords of congruent circles subtend equal angles at their centres.

Question 2: Prove that if chords of congruent circles subtend equal angles at their centres, then the chords are equal.

Answer: Given: Chords of congruent circles subtend equal angles at their centres.

To prove: Then the chords are equal

Let us consider two congruent circles (circles of same radius) with centres as O and O’.

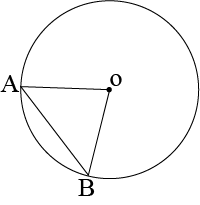
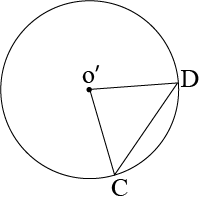
In $\triangle AOB$ and $\triangle COD$,

$\angle AOB=COD$  (Given)

$OA=O’C$  (Radius of congruent circles) $OB=OD$  (Radii of congruent ciorcles)

$∴\triangle≅\triangle COD$ (SAS congruence rule)

$⇒AB=CD$  (By CPCT)

Hence, if the chords of congruent circles subtend equakl angles at their respective centres, then the chors are equal. 

Exercise 9.2:

Question 2: Two circles of radii 5 cm and 3 cm intersects at two points and the distance between their centres is 4 cm. Find the length of the common chord.

Answer: 

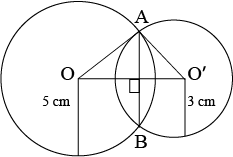
Consider the radius of the circle with centre as $O$ and $O’$ 5c m and 3 cm respectively.

$OA=OB=5\space cm$  (Radius of same circle)

$OA=OB=3\space cm$  (Radius of same circle)

$OO’$ will be the perpendicular bisects of chord $AB$

$∴AC=CB$

It is given that, $OO’=4\space cm$

Let the length of $OC$ be $x$ cm. Therefore, $O’C\0 will be \((4-x)$ cm.

In $\triangle OAC$,

$\angle ACO$ is a right angle. Therefore,

Using Pythagoras theorem,

$OA^2=AC^2+OC^2$

\9⇒5^2=AC^2+x^2\)

$⇒25-x^2=AC^2$   …(1)

In $\triangle OAC$,

$\angle ACO’$ is a right angle.

Therefore,

Using Pythagoras theorem,

$O’A^2=AC^2+OC^2$

$⇒3^2=AC^2+(4-x)62$

$⇒9=AC^2+16+x^2-8x$

$⇒AC^2+x^2-7+8x$  …(2)

From equation (1) and (2), we get

$25-x^2=-x^2-7+8x$

$8x=32$

$x=4$

Putting the value of $x$ in equation (1), we get

$AC^2=25-4^2$

$AC^2=25-16$

$AC^2=9$

$AC=3$

Since,

$AB=2\times AC$

$AB=2\times 3$

$AB=6\space cm$

Therefore, the common chord of both the circles will pass through the centre of the smaller circle i.e, $O’$ and hence, it will be the diameter of the cmaller circle.

Question 2: If two chord of a circle intersect within the circle, prove that the segments of one chord are equal to corresponding segments of the other chord.

Answer: Let $RS$ $PQ$ be two chords of equal lengths of a given circle, and they are intersecting each other at point $T$.

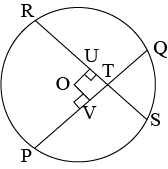
Construct two perpendicular lines $OV$ and $OU$ on these chords.

In $\triangle OVT$ and $\triangle OUT$,

\(Since equal chors of a circle are equidistant from the centre. Therfore,

$OV=OU$

$\angle OVT=\angle OUT=90^0$

The side $OT$ is present in borth triangles. Therefore,

$OT=OT$  (Common)

$∴OVT≅\triangle OUT$  (By RHS axiom of congruency)

Hence $VT=UT$   …(1)

As they are corresponding parts of the corresponding triangles.

It is also given that $PQ=RS$  …(2)

$⇒\frac{1}[2}PQ=\frac{1}{2}RS$

$⇒PV=RU$   …(3)

On adding Equation (1) and (3), we obtain

$PV+VT=RU+UT$

$⇒PT=RT$      ….(4)

On subtracting Equation (4) from Equation (2), we obtain

$PQ-PT=RU+UT$

$⇒QT=ST$   …(5)

From equation (4) and (5) we can conclude that the corresponding segments of chords $PQ$ and $RS$ are congruent to each other.

Question 3: If two equal chords of a circle intersect within the circle, prove that the line joining the point of intersection to the centre makes equal angle with the chords.

Answer: Let $RS$ and $PQ$ be two chords of equal lengths of a given circle and they are intersect each other at point $T$.

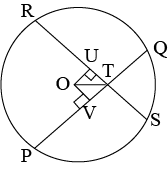
Construct two perpendicular lines $OV$ and $OU$ on these chords.

In $\triangle OVT$ and $\triangle OUT$

Since equal chors of a circle are equidistant from the centre. Therfore,

$OV=OU$

$\angle OVT=\angle OUT=90^0$

The side $OT$ is present in both triangles. Therefore,

$OT=Ot$  (Common)

$∴\triangle OVT≅\triangle OUT$  (By RHS aciom of congruency)

Hence $\angle OTV=\angle OTU$

As they are corresponding parts of the corresponding triangles.

Therefore, it can be concluded from above that the line joining the point of intersection to the centre makes equal angles with the chords.

Question 4: If a line intersects two concentric circles (circles with the same centre) with cnetre $O$ at $A,B,C$ and $D$, prove that $AB=CD$ (see figure).

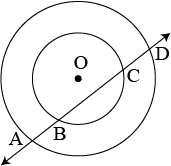
Answer: Construct a perpendicular line $OM$ on line $AD$.

It can be observed that the chord of the smaller circle is $BC$, and the chord of the bigger circle is $AD$

Perpendicular drawn from the centre of the circle bisects the chord.

$∴BM=MC$  …(1)

And $AM=MD$  …(2)

On subtracting Eqation (2) from (1), we obtain

$AM-BM=MD-MC$

$∴AB=CD$

Question 5: Three girls Reshma, Salma and Mandip are playing a game by standing on a circle of radius 5 m drawn in a park. Reshma throws a ball to Salma, Salma to Mandip, Mandip to Reshma. If the distance between Reshma and Salma and between Salma and Mandip is 6 m each, what is the distance between Reshma and Mandip? 

Answer: Construct two perpendicular line $OA$ and $OB$ on line $RS$ and $MS$ respectively.

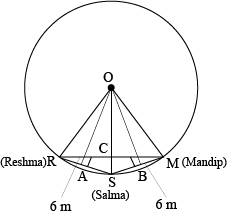
$AR=AS=\frac{6}{2}=3\space m$

$OR=OS=OM=5\space m$  (Radii of the same circle)

In $\triangle OAR$

Using Pythagoras theorem,

$OA^2+AR^2=OR^2$

$⇒OA^2+(3m)^2=(5m)^2$

$⇒OA^2=(25-9)m^2=16\space m^2$

$⇒OA=4\space m$

$ORSM$ will be a kite as pair of adjacent sides ae equal (OR=OM and (RS=SM). Since the digonals of kite are perpendicular and the diagonal common to both side isosceles triangle is bisected by anothe diagonal.

$\angle RCS$ will be of $90^0$ and $RC=CM$

Area of $\triangle ORS=\frac{1}{2}\times OA\times RS$

$⇒\frac{1}{2}\times RC\times OS=\frac{1}{2}\times 4\times 6$

$RC\times 5=24$

$⇒RC=4.8$

$RM=2RC=2(4.8)=9.6\space m$

Therefore, Reshma and Mandip are $9.6\space m$ apart.

Question 6: 6. A circular park of radius 20 m is situated in a colony. Three boys Ankur, Syed and David are sitting at equal distance on its boundary each having a toy telephone in his hands to talk each other. Find the length of the string of each phone.

Answer: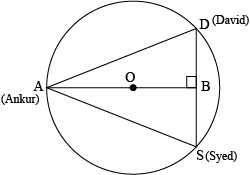

All the side of the triangle are equal. Therefore,

$\triangle ASD$ is an equilateral triangle.

$OA (radius)=2\space m$

Since, circumcentre(O) is the point of intersection of all the medians of equilateral triangle ASD. We also know that medians intersect each other in the ratio 2:1. Since AB is the median of equilateral triangle ASD, we can write it as,

$⇒\frac{OA}{OB}=\frac{2}{1}$

$\frac{20\space m}{OB=\frac{2}{1}$

$⇒OB=(\frac{20}{2})=10\space m$

$AB=OA+OB=(20+10)\space m=30\space m$

In $\triangle ABD$,

Using Pythagoras theorem,

$AD^2=AB^2+BD^2$

\⇒AD^2=(30)^2+(\frac{AD}{2})^2\)

$⇒AD^2=900+\frac{1}{4}AD^2$

$⇒\frac{3}{4}AD^2=900$

$⇒AD^2=1200$

$AD=20\sqrt3\space m$

Therefore, the length of the string of each phone will be $20\sqrt3\space m$.

Exercise 9.3:

Question 1: In the given figure, A, B and C are three points on a circle with center O sych that $\angle BOC=30^0$ and $\angle AOB=60^0$. If $D$ is a pont on the circle other than the arc $ABC$, find $\angle ADC$.

Answer: 

We can notice that,

$\angle AOC=\angle AOB+\angle BOC$

$=60^0+30^0$

$=90^0$

Now, recall that subtended angle at its centre is double the angle it has at any point on the remaining section of the circle.

Thus,

$\angle ADC=\frac{1}{2}\angle AOC$

$=\frac{1}{2}\times90^0$

$=45^0$

Hence, $\angle ADC=45^0$

Question 2: A chord of a circle is equal to the radius of the circle. Find the angle subtended by the chord at a point on the minor arc and also at a point on the major arc.

Answer: 

By the given information, in $\triangle OAB$,

$AB=OA=OB$, since each is a radius of the circle.

Therefore, the triangle $\triangle OAB$ is equilateral.

So, the value of each of the interior angles of $\triangle AOB$ is $60^0$.

That is, $\angle AOB=60^0$

$⇒\angle ACB=\frac{1}{2}\angle AOB$

$=\frac{1}{2}\times 60^0$

$=30^0$

Now, in the cyclic quadrilateral $ACBD$

$\angle ACB+\angle ADB=180^0$, since the sum of the opposite angles in cyclic quadrilateral is $180^0$.

$⇒\angle ADB=180^0-30^0=150^0$

Hence, the chord’s angle at the points on the minor arec and on the major arc, respectively, are $30^0$ and $150^0$

Question 3: In the given figure, $\angle PQR=90^0$, where $O,\space Q$ and $R$ are points on a circle with center $O$. Find $\angle OPR$

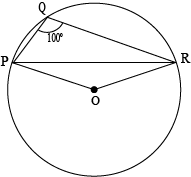
Answer: 

First, take $PR$ as a chord of the circle centered at $O$.

Then, consider any point $S$ on the major arc of the circle.

Therefore, we get the equilateral quadrilateral $PQRS$.

So, $\angle PQR+\angle PSR=180^0$, since the sum of the opposite angles of cyclic quadrilateral is $180^0$

$⇒\angle PSR=180^0-90^0=80^0$

Now, it is generally known that the angle subtended by an arc at the center is twice the angle subtended by it at any point on the remaining part of the circle.

Thus,

$\angle POR=2\angle PSR=2\times80^0=160^0$

Then, in the triangle $\triangle POR$,

$OP=OR$, since each of them are radius of the circle.

$\angle OPR=\angle ORP$, angles opposite to the equal sides of the traingle.

Therefore,

$\angle OPR+\angle ORP+\angle POR=180^0$, by the angle sum propery of a triangle.

$⇒2\angle OPR+160^0=180^0$

$⇒2\angle OPR=180^0-160^0=20^0$

Hence, $\angle OPR=9^0$

Question 4: In figure $9.38,\space \angle ABC=69^0,\space \angle ACB=31^0$, find $\angle BDC?$

Answer:

In the $\triangle ABC$,

$\angle BAC+\angle ABC+\angle ACB=180^0$, by the angle sum property of a circle.

$⇒\angle BAC+69^0+31^0=180^0$

$⇒\angle BAC=180^0-90^0$

$⇒\angle BAC=80^0$

Now, it is known that angles in the same segment of the circle are equal. So here$\angle BAC=\angle BDC$

Hence, $\angle BDC=80^0$

Question 5: In the given figure, $A,\space B,\space C$ and $D$ are four points on a circle $AC$ and $BD$ intersect at a point $E$ such that $\angle BEC=130^0$ and $\angle ECD=20^0$. Find $\angle BAC$.

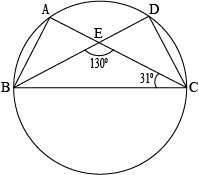
Answer: 

it is knwon that , the exterior angle equals the sum of the opposite niterior angles.

So, in the triangle $\triangle CDE$

$\angle CDE+\angle DCE=\angle CEB$

Therefore,

$\angle CDE+20^0130^0$

$⇒\angle CDE=19^0$

Again, since the angles $\angle BAC$ and $\angle CDE$ are in the same segment of the circle, so $\angle BAC=\angle CDE$

Hence, $\angle BAC=19^0$

Question 6: $ABCD$ is a cyclic quadrilateral whose diagonals intersect at a point $E$. If $\angle DBC=70^0,\space \angle BAC=30^0$, find $\angle BCD$. Further, if $AB=BC$ , find $\angle ECD$.

Note that, here the angles $\angle ECB$ and $\angle CAD$ are in the same segment of the circle.

So, $\angle CBD=\angle CAD=70^0$

Now, $\angle BAD=\angle BAC+\angle CAD=30^0+70^0=90^0$

Also, since sum of the opposite angles in a cyclic quadrilateral is $180^0$, so

$\angle BCD+\angle BAD=180^0$

$⇒\angle BCD+90^0=180^0$

$\angle BCD=180^0$

Again, in the triangle $\triangle ABC$,

$AB=AB$,

$\angle BCA=\angle CAB$, since angle opposite to equal sides of triangle are equal.

Therefore, $\angle BCA=30^0$

Now, $\angle BCD=80^0$

$⇒\angle BCA+\angle ACD=80^0$

$⇒30^0\angle ACD=80^0$

$⇒\angle ACD=50^0$

Hence, $\angle ECD=50^0$

Question 7: If diagonals of a cyclic quadrilateral are diameters of the circle through the vertices of the quadrilateral, prove that it is a rectangle.

Anaswer: 

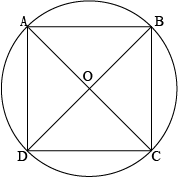
Suppose that $ABCD$ is a cyclic quadilateral whose diagonals $BD$ and $AC$ intersecting each other at point $O$.

Then, $\angle BAD=\frac{1}{2}\angle BOD=\frac{180^0}{2}=90^0$  (The angle athe circumference in a semicircle).

Also, $\angle BCD$ and $\angle BAD$ are opposite angles in the cyclic quadrilateral.

So, $\angle BCD+\angle BAD=180^0$

$⇒\angle BCD=180^0-90^0=90^0$

Therefore,

$\angle ADC=\frac{1}{2}\angle ACO=\frac{1}{2}\times180^0=90^0$ (The angle at the circumference in a semicircle)

Also, $\angle ADC+\angle ABC=180^0$, since $\angle ADC,\space \angle ABC$ are the oppositing angles in the cyclic quadrilateral.

$⇒90^0+\angle ABC=180^0$

$⇒\angle ABC=90^0$

Hence, all the interior angles of a cyclic quadrilateral is of $90^0$ and so it is a rectangle.

Question 8: If the non-parallel sides of a trapezium are equal, prove that it is cyclic.

Answer: 

Let $ABC$ is a trapezium such that $AB\parallel CD$ and $BC=AD$.

Now, draw pependicular lines $AM$ and $BN$ on the line $CD$

Then, in the triangles $\triangle AMD$ and $\triangle BCN$,

$AD=BC$  (provided)

$\angle AMD=BNC$, by the formation, each angle is $90^0$

$AM=BN$, since $AB\parallel CD$

Thus, $\triangle AMD≅\triangle BNC$  (by S-A-S congruence rule)

Therefore,

$\angle ADC=\angle BCD$  (Corresponding angle of congruence triangle) ..(i)

Also, $\angle BAD+\angle ADC=180^0$  (The angles are on the sam side)

$⇒\angle BAD+\angle BCD=180^0$, by the equation (i)

Thus, the sum of the opposite angles is $180^0$

Hence, $ABCD$ is cyclic quadrilateral

Question 9: Two circles inatersect at two point $B$ and $C$. Through $B$, two-line segments $ABD$ and $PBQ$ are drawn to intersect the circles at $A,\space D$ and $P,\space Q$ respectively (see the given figure). Prove that $\angle ACP=\angle QCD$

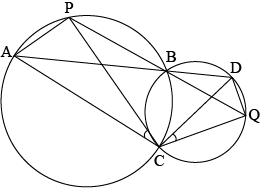
Answer: 

First, join the chors $AP,\space DQ$.

Then, $\angle PBA=\angle ACP$, (Thus angles are on the chord AP) ..(i)

And $\angle DBQ=\angle QCD$  (The angles are on the chord DQ)  ..(ii)

Now, the line segment $ABD$ and $PBQ$ intersects at the point $B$

So, $\angle PBA=\angle DBQ$  …(iii)

(since, $\angle PBA,\space \angle DBQ$ are vertically opposite angles)

Then the equation (i), (ii) anf (iii) yields

$\angle ACP=\angle QCD$

Question 10: If circles are drawn taking two sides of a triangle as diameters, prove that the point of intersection of these circles lie on the third side. 

Answer: 

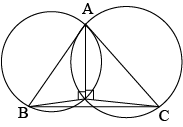
Let $\triangle ABC$ be a triangle.

By the given information, two circles intersect each other in such a way that $AB$ and $AC$ are diameters.

If possible, let the circles interesect at the point $D$, that does not lie on the line $BC$

Now, join the line $AD$

Then, $\angle ADB=90^0$, since it is an angle subtended by semicircle.

Similarly, $\angle ADC=90^0$

Therefore, $\angle BDC=\angle ADB+\angle ADC=90^0+90^0=180^0$

Thus, $BDC$ is a strraight line and so, it is a contradiction.

Hence, the point of intersection of the circles lies on the third side $BC$ of the triangle $\triangle ABC$.

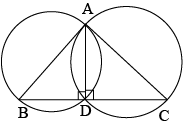
Question 11: $ABC$ and $ADC$ are two right triangles with common hypotenuse $AC$. Prove that $\angle CAD=\angle CBD$

Answer: 

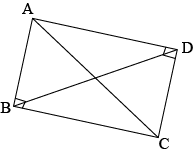
In $\triangle ABC$, we have

$\angle ABC+\angle BCA+\angle CAB=180^0$, by the angle sum property.

$⇒90^0+\angle BCA+\angle CAB=180^0$

$⇒\angle BCA+\angle CAB=90^0$   ..(i)

Again, in the triangle $\triangle ADC$, we obtain

$\angle CDA+\angle ACD+\angle DAC=180^0$, by the angle sum property.

$⇒90^0+\angle ACD+\angle DAC=180^0$ 

$⇒\angle ACD+\angle DAC=90^0$ ….(ii)

Now, adding (i) and (ii), yieds,

$\angle BCA+\angle CAB+\angle ACD+\angle DAC=180^0$

$⇒(\angle BCA+\angle ACD)+(\angle CAB+\angle DAC)=180^0$

$⇒\angle BCD+\angle DAB=180^0$  …(iii)

Also, we are provided that,

$\angle B+\angle D=90^0+90^0=180^0$   ..(iv)

By observing the equations (iii) and (iv), it can be concluded that since the sum of the measures of opposite angles of quadrilateral $ABCD$ is $180^0$, so it must be a cyclic quadrilateral.

Thus, $\angle CAD=\angle CBD$, since both the angles are on the chord $CD$.

hence, the required result is proved.

Question 12: Prove that a cyclic parallelogram is a rectangle.

Answer:

Consider that cyclic parallelogram $ABCD$

The, $\angle A+\angle C=180^0$ (Opposite angle of the cyclic quadrilateral) …(i)

Again, in a parallelogram, opposite angles are the same.

Therefore, $\angle A=\angle C$ and $\angle B=\angle D$

So, the equation (i) and be written as

$\angle A+\angle C=180^0$

$⇒\angle A+\angle A=180^0$

$⇒2\angle A=180^0$

$⇒\angle A=90^0$

Thus, one interior angle of the parallelogram $ABCD$ is of $90^0$. That means, it is a rectangle.

Hence, it is proved that a cyclic parallelogram is a rectangle.