NCERT Solutions for Maths Class 9 Chapter 7

EXERCISE 7.1

Question 1: In quadrilateral \(ACBD,\space AC=AD\) and \(AB\) \(\angle A\) (See the given figure). Show thatn \(\triangle ABC≅\triangle ABD\). What can you about \(BC\) and \(BD\)?

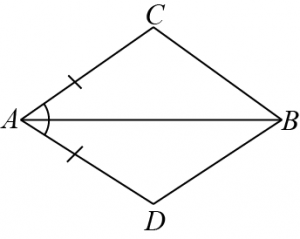
Answer: Given: In quadrilateral \(ACBD,\space AC=AD\) and \(AB\) is bisected by \(\angle A\).

To find: show that \(\triangle ABC≅ABD\).

In \(\triangle ABC,\space \triangle ABD\)

\(AC=AD\) (Given)

\(\angle CAB=\angle DAB\)  (\(AB\) bisect \(\angle A\))

\(AB=AB\)  (Common)

\(∴\triangle ABC≅\triangle ABD\)  (By \(SAS\) congruence rule)

\(∴BC=BD\)  (by \(CPCT\))

Therefore, \(BC\) and \(BD\) are of equal lengths.

Question 2: \(ABCD\) is a quadrilateral in which \(AD=BC\) and \(\angle DAB-\angle CBT\)  (See the given figure) Prove that

(i) \(\triangle ABD≅\triangle BAC\)

(ii) \(BD=AC\)

(iii) \(\angle ABD=\angle BAC\)

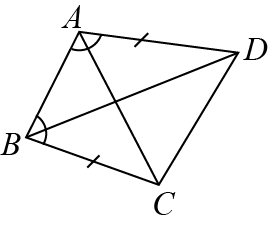
Answer: Given: \(ABCD\) is a quadrilateral where \(AD=BC\) and \(\angle DAB=\angle CBA\)

To prove:

(i) \(\triangle ABD≅\triangle BAC\)

(ii) \(BD=AC\)

(iii) \(\angle ABD=\angle BAC\)

In \(\triangle ABD,\space \triangle BAC\),

\(AD=BC\) (Given)

\(\angle DAB=\angle CBA\) (Given)

\(AB=BA\)  (Common)

\(∴\triangle ABD≅\triangle BAC\) (By \(SAS\) congruence rule)

\(∴BD=AC\)  (By \(CPCT\))

\(\angle ABD=\angle BAC\) (By \(CPCT\))

Question 3: \(AD\) and \(BC\) are equal perpendiculars to a line segment \(AB\) (See the given figure), Show that \(CD\) bisects \(AB\).

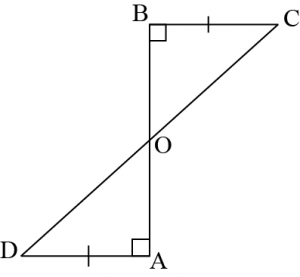
Answer: Given: \(AD\) and \(BC\) are equal perpendiculars to a line segment \(AB\)

To prove: \(CD\) bisects \(AB\)

In \(\triangle BOC,\space \triangle AOD\),

\(\angle BOC=\angle AOD\) (Vertically opposite angles)

\(\angle CBO=\angle DAO\) Each right angles)

\(BC=AD\)  (Given)

\(∴\triangle BOC≅\triangle AOD\)  (\(AAS\) congruence rule)

\(∴BO=AO\)  (By \(CPCT\))

\(⇒CD\) bisects \(AB\).

Question 4: \(l\) and \(m\) are two parallel lines intersected by another pair of parallel lines \(p\) and \(q\) (see the given figure). Show that \(\triangle ABC≅\triangle CDA\).

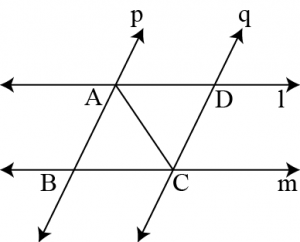
Answer:

Given: \(l\) and \(m\) are two parallel lines intersected by another pair of parallel lines \(p\) and \(q\) to prove: \(\triangle ABC≅\triangle CDA\)

In \(\triangle ABC,\space \triangle CDA\),

\(\angle BAC=\angle DCA\)  (Alternate interior angle, as \(p\parallel q\))

\(2AC=CA\)  (Common)

\(\angle BCA=\angle DAC\)  (Alternate interior angles, as \(l\parallel m\))

\(∴\triangle ABC≅\triangle CDA\)  (By \(ASA\) congruence rule)

Question 5: Line \(l\) is the bisector of an angle \(\angle A\) and \(B\) is anu point on \(l\). \(BP\) and \(BQ\) are perpendiculars from \(B\) to the arms of \(\angle A\) (see the given figure), Show that:

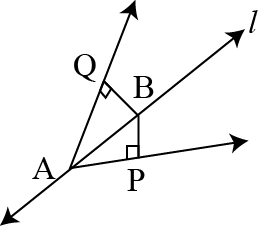
(i) \(\triangle APB≅\triangle AQB\)

(ii) \(BP=BQ\) of \(B\) is equidistant from the arem of \(\angle A\).

Answer: 

Given: Line \(l\) is the bisector of an angle \(A\) and \(\angle B\) is any point on \(l\).

To prove: (i) \(\triangle APB≅\triangle AQB\)

(ii) \(BP=BQ\) or \(B\) is equidistant from the arms of \(\angle A\)

In \(\triangle ABP,\space \triangle AQB\)

\(\angle APB=\angle AQB\)  (Each right angle)

\(\angle PAB=\angle QAB\)  (\(l\) is the angle bisector \angle A\))

\(AB=AB\) (Common)

\(∴\triangle APB≅\triangle AQB\)  (By\(AAS\) congruence rule)

\(∴BP=BQ\)  (By\(CPCT\))

Or, it can be said that \(B\) is equidistant form the arms of \(\angle A\).

Question 6: In the given figure, \(AC=AE,\space AB=AD\) and \(\angle BAD=\angle EAC\). Show that \(BC=DE\)

Answer: 

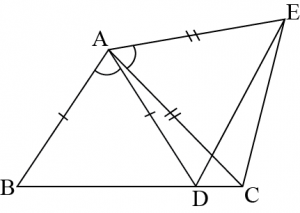
Given:  \(\angle BAD=\angle EAC\)

To prove: \(BC=DE\)

it is given that

\(\angle BAD=\angle EAC\)

\(\angle BAD+\angle DAC=\angle EAC+\angle DAC\)

\(\angle BAC=\angle DAE\)

In \(\triangle BAC,\space \triangle DAE\)

\(\angle BAC=\angle DAE\)  (Proved above)

\(AC=AE\)  (Given)

\(∴\triangle BAC≅\triangle DAE\)  (By \(SAS\) congruence rule)

\(∴BC=DE\) (By \(CPCT\))

Question 7: \(AB\) is a line segment and \(P\) is its mid-point. \(D\) and \(E\) are points on the same side of \(AB\) such that \(\angle BAD=\angle ABE\) and \(\angle EPA=\angle DPB\) (See the given figure). Show that

(i) \(\triangle DAP≅\triangle EBP\)

(ii) \(AD=BE\)

Answer: 

Given: \(AB\) is line segment and \(P\) is its mid-point. \(D\) and \(E\) are points on the same side of \(AB\) such that \(\angle BAD=\angle ABE\) and \(\angle EPA=\angle DPB\)

Tor prove:

(i) \(\triangle DAP≅\triangle EBP\)

(ii) \(AD=B\)

it is given that

\(\angle EPA=\angle DPB\)

\(\angle EPA+\angle DPE=\angle DPB+\angle DPE\)

\(∴\angle CPA=\angle EPB\)

In \(\triangle DAP,\space \triangle EBP,\space \angle DAP=\angle EBP\) (Given)

\(AP=BP\)  (\(P\) is mid-point \(AB\))

\(\angle PDA=\angle EPB\)  (From above)

\(∴\triangle DAP≅\triangle EBP\)  (\(ASA\) congruence rule)

\(∴AD=BE\) (By \(CPCT\))

Question 8: In right traingle \(ABC\), right angled at \(C,\space M\) is the mid-point of hypotenuse \(AB\). \(C\) is joined to \(M\) and produced toa point \(D\) such that \(DM=CM\). Point \(D\) is joined to point \(B\) (See the given figure). Show that:

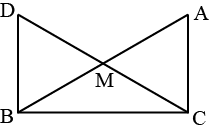
(i) \(\triangle AMC≅\triangle BMD\)

(ii) \(\angle BDC\) is a right angle

(iii) \(\triangle ABC≅\triangle ACB\)

Answer: Given: \(M\) is the mid-point of hypotenuse \(AB.\space DM=CM\)

(i) In \(\triangle AMC,\space \triangle BMD\)

\(AM=BM\)  (\(M\) is the mid-point of \(AB\))

\(\angle AMC=\angle BMD\)  (vertically opposite angles)

\(CM=DM\) (Given)

\(∴\triangle AMC ≅\triangle BMD\)  (By SAS congruence rule)

\(∴AC=BD\)  (By CPCT)

(ii) \(\angle ACM=\angle BDM\)

Howevere, \(\angle ACM,\space \angle BDM\) are alternate interior angles.

Since alternate angle are equal, it can be said that \(DB\parallel AC\)  (Co-interior angles)

(iii) In \(\triangle DBC,\space \triangle ACB\),

\(DB=AC\)  (Already proved)

\(\angle DBC=\angle ACB\) (Each \(90^0\))

\(BC=CB\) (Common)

\(∴\triangle BDC≅\triangle ACB\) (SAS congruence rule)

(iv) \(∴\triangle DBC≅\triangle ACB\)

\(AB=DC\)  (By CPCT)

\(AB=2\space CM\)

\(CM=\frac{1}{2}AB\)

Exercise 7.2

Question 1: In an isosceles triangle \(ABC\), with \(AB=AC\), the bisectors of \(\angle B\) and \(\angle C\) intersect each other at \(O\). Join \(A\) to \(O\). show that:

(i) \(OB=OC\)

(ii) \(AO\) bisects \(\angle A\)

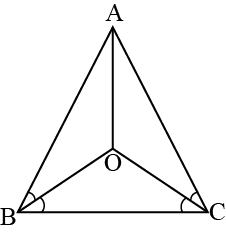
(i) \(OB=OC\)

Answer: It isgiven that in triangle \(ABC\) is an isosceles triangle with \(AB=AC\).

\(∴\angle ACB=\angle ABC\) (Angles opposite to equal sides of a triangle are equal)

Multiplying \(\frac{1}{2}\) on both sides, we get

\(\frac{1}{2}\angle ACB=\frac{1}{2}\angle ABC\)

\(\angle OCB=\angle OBC\)

\(∴OB=OC\) (Sides opposite to equal angles of a triangle are alos equal)

(ii) \(AO\) bisects \(\angle A\)

In \(\triangle OAB\) and \(\triangle OAC\)

Side \(AO\) is present in both triangle. Therefore,

\(AO=AO\) (Common)

Length of side \(AB\) is equal to \(AC\), i.e., \(AB=AC\) (Given)

\(OB=OC\) (Proved above)

Therefore,

\(\triangle OAB≅\triangle OAC\) (By SSS axiom of congruency)

Therefore, \(\angle BAO=\angle CA)\).

As they are corresponding parts of the corresponding triangle.

\(∴AO\) busects \(\angle A\).   (\(angle BAO=\angle CAO\))

Question 2: In \(\triangle ABC,\space AD\) is the perpendicular busector of \(BC\) (see the given figure). Show that \(\triangle ABC\) is an isosceles triangle in which \(AB=AC\).

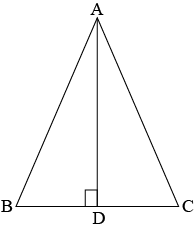
Answer: 

In \(\triangle ADC\) and \(\triangle ADB\)

Side \(AD\) is present in both triangle.

\(∴AD=AD\)  (Common)

Since \(AD\) is the perpendicular bisector of \(BC\).

\(\angle ADC=\angle ADB=90^0\) and \(CD=BD\)

\(∴\triangle ADC≅\triangle ADB\)  (By SAS axion of congruency)

Therefore, \(AB=AC\)

As they are corresponding parts of the corresponding triangle.

Hence, \(\triangle ABC\) is an isosceles triangl as two of it’s sides are equal, i.e., \(AB=AC\)

Question 3: \(ABC\) is an isosceles triangle in which altitudes \(BE\) and \(CF\) are frawn to equal sides \(AC\) and \(AB\) respectively (See the given figure). Show that these altitudes are equal.

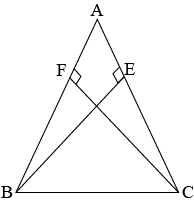
Answer: In \(\triangle AEB\) and \(\triangle AFC\) 

Since \(BE\) and \(CF\) are drawn to equal side \(AC\) and \(AB\). Therefore,

\(\angle AEB\) and \(\angle AFC\) (Each \(90^0\)

As \(\angle A\) lies in both the triangles. Therefore,

\(\angle A=\angle A\)  (Common angle)

Length of side \(AB\) is equal to \(AC\), i.e., \(AB=AC\)  (Given)

\(∴\triangle AEB≅\triangle AFC\)  (By AAS axiom of congruency)

Therefore, \(BE=CF\).

As they are corresponding parts of the corresponding triangle.

Question 4: \(ABC\) is a triangle in which altitudes \(BE\) and \(CF\) to sides \(AC\) and \(AB\) are equal (see the given figure). Show that

(i) \(\triangle ABE≅\triangle ACF\)

(ii) \(AB=AC\), i.e., \(ABC\) is an isosceles triangle.

(i) \(\triangle ABE≅\triangle ACF\)

\(ABC\) is a triangle in which altitudes \(BE\) and \(CF\) to sides \(AC\) and \(AB\).

Therefore, \(\angle ABE\) and \(\angle ACF=90^0\)

Since \(\angle A\) is present in both triangles,

\(∴\angle A=\angle A\)  (Common angle)

Length of side \(BE\) is equal to \(CF\), i.e., \(BE=CF\) (Given)

\(∴\triangle ABE≅\triangle ACF\)  (proved above)

Therefore, \(AB=AC\).

As they are corresponding parts of the corrresponding triangle.

Question 5: \(ABC\) and \(DBC\) are two isosceles triangles triangles on the same base \(BC\) (see the given figure), Show that \(\angle ABD=\angle ACD\)

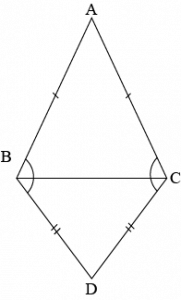
Answer: 

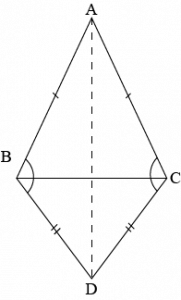
Construction: Join \(AD\)

In \(\triangle ABD\) and \(\triangle ACD\),

Length of side \(AB\) is equal to \(AC\), i.e., \(AB=AC\)  (Given)

Length of side \(BD\) is equal to \(CD\), i.e., \(BD=CD\)  (Given)

As side \(AD\) is present in both triangles. Therefore,

\(AD=AD\)  (Common)

\(∴\triangle ABD≅\triangle ACD\)  (By SSS acion of congruency)

Therefore, \(\angle ABD=\angle ACD\)

As they are corresponding parts of the corresponding triangle.

Question 6: \(\triangle ABC\) is an isosceles tringle in which \(AB=AC\). Side \(BA\) is produced to \(D\) such that \(AD=AB\)  (see the given figure). SHow that \(\angle BCD\) is a right angle.

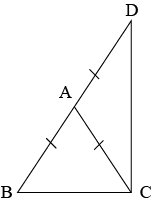
Answer: In \(\triangle ABC\),

Length of side \(AB\) is equal to \(AC\), i.e., \(AB=AC\)  (Given)

\(∴\angle ACB=\angle ABC\) (angles opposite to equal sides of a triangle are also equal)

In \(\triangle ACD\),

Length of side \(AC\) is equal to \(AD\), i.e., \(AC=AD\) (Given)

\(∴\angle ADC=\angle ACD\)  (Angles opposite to equal sides of a triangl are also equal)

In \(\triangle BCD\),

\(\angle ABC+\angle BCD+\angle ADC=180^0\)  (Sum of angles in a triangles is \(180^0\)

\(\angle ACB+\angle ACB+\angle ACD+\angle ACD=180^0\)   (\(\angle BCD=\angle BCA+\angle ACD\))

\(2(\angle ACD+\angle ACD)=180^0\)

\(2(\angle BCD)=180^0\)

\(∴\angle BCD=90^0\)

Question 7: \(ABC\) is a right-angles triangle in which \(\angle A=90^0\) and \(AB=AC\). Find \(\angle B\) and \(\angle C\)

Answer: 

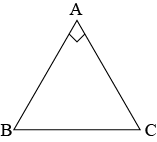
It is given that the side \(AB=AC\)

Angles opposite to equal sides are also equal

\(∴\angle C=\angle B\)   …(i)

In \(\triangle ABC\),

\(\angle A+\angle B+\angle C=180^0\)  (Sum of angle in a triangle is \(180^0\)) 90^0+\angle B+\angle C=180^0\) ….. from equation (i)

\(90^0+\angle B+\angle B=180^0\)

\(2\angle B=90^0\)

\(\angle B=45^0\)

Because \(\angle B=\angle C\)   .. from equation (i)

\(∴\angle C=45^0\)

Question 8: Show that the abgles of a n equilateral triangle are \(60^0\) each.

Answer: 

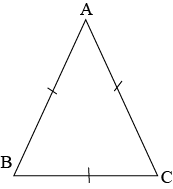
Consider that \(ABC\) is an equilateral triangle in which all sides are equal.

Therefore, \(AB=ABC=AC\)

\(AB=AC\)

Angles oppiste to equal sidea of a triangle are equal

\(∴\angle C=\angle B\)   …. (i)

Also, \(AC=BC\)

Angles opposite to equal sides of a triangl are equal

\(∴\angle B=\angle A\)   ..(ii)

Therefore, from equation (i) and (ii), we get

\(\angle A=\angle B=\angle C\)   ….(iii)

In \(\triangle ABC\),

\(\angle A+\angle B+\angle C=180^0\)    (Sum of angles in a triangle is \(180^0\))

\(\angle A+\angle B+\angle C=180^0\)   … from equation (iii)

\(3\angle A=180^0\)

\(\angle A=60^0\)

\(∴\angle A=\angle B=\angle C=60^0\)

From above we can conclude that all interior angles of an equilateral triangl has an angle of \(60^0\).

Excercise 7.3

Question 1: \(\triangle ABC\) and \(\triangle DBC\) are two isosceles triangles on the ssame base \(BC\) and vertices \(A\) a \(D\) are on the same side of \(BC\) (see the given figure). If \(AD\) is extended to intersect \(BC\) at \(P\), show that:

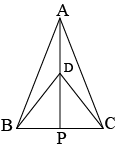
(i) \(\triangle ABD≅\triangle ACD\)

Answer: In \(\triangle ABD\) and \(\triangle ACD\),

\(AB=AC\)  (Given)

\(BD=CD\)  (Given)

\(AD=AD\)  (Common) Therefore,

\(\triangle ABD≅\triangle ACD\)  (by SSS rule)

\(\angle BAD=\angle CAD\)   (By CPCT)

\(\angle BAP=\angle CAP\)

(ii) \(\triangle ABP≅\triangle ACP\)

Answer: In \(\triangle ABP\) and \(\triangle ACP\),

\(AB=AC\)  (Given)

\(\angle BAP=\angle CAP\)

\(AP=AP\)  (Common)

Therefore,

\(\triangle ABP≅\triangle ACP\)   (By SAS congruence rule)

Therefore, \(BP=CP\)   (By CPCT)

(iii) \(AP\) bisects as well as \(\angle D\).

Answer: Since, \(\angle BAP=\angle CAP\),

Therefore, \(AP\) bisects \(\angle A\)

In \(\triangle BDP\) and \(\triangle CDP\),

\(BD=CD\)  (given)

\(DP=DP\)  (Common)

\(BP=CP\)

Therefore,

\(\triangle BDP≅\triangle CDP\)  (By SSS congruence rule)

Therefore, \(\angle BDP=\angle CDP\)  (By CPCT)

Hence, \(AP\) bisects \(\angle D\)

(iv) \(AP\) is the perpendicular bisector of \(BC\).

Answer: Since \(\triangle BDP≅\triangle CDP\),

Therefore, \(\angle BPD=\angle CPD\)  (By CPCT)

\(\angle BPD+\angle CPD=180^0\)  (Linear pair of angles)

\(\angle BPD+\angle BPD=180^0\)  (Since \(\angle BDP=\angle CDP\))

\(\angle BPD=90^0\)

Hence \(AP\) is the perpendicular bisector of \(BC\).

Question 2: \(AD\) is an altitude of an isosceles triangles \(ABC\) in which \(AB=AC\). Shwo that:

(i) \(AD\) bisects \(BC\)

Answer: In \(\triangle ABC\) and \(\triangle CAD\),

\(\angle ADB=\angle ADC\)  (Each \(90^0\))

\(AB=AC\)  (Given)

\(AD=AD\)  (Common)

Therefore,

\(\triangle BAD≅\triangle CAD\)  (By RHS congruence rule)

Therefore,

\(BD=CD\)  (By CPCT)

hence \(AD\) bisects \(BC\).

(ii) \(AD\) bisects \(\angle A\)

Answer: 

Also, \(\angle BAD=\angle CAD\)  (By CPCT)

Hence, \(AD\) bisects \(BC\).

Therefore, \(AD\) bisects \(\angle A\)

Question 3: Two sides \(AB\) and \(BC\) and median \(AM\) of one triangle \(ABC\) are respectively equal to sides \(PQ\) and \(QR\) and median \(PN\) of \(\triangle PQR\) (see the given figure). Show that:

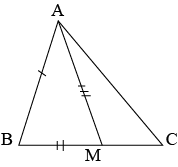
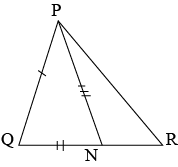
(i) \(\triangle ABM≅\triangle PQN\)

Answer: In \(\triangle ABC,\space AM\) is the median to \(BC\).

Therefore,

\(BM=\frac{1}{2}BC\)

In \(\triangle PQR,\space PN\) is the median \(QR\).

Therefore,

\(QN=\frac{1}{2}QR\)

However,

\(BC=QR\)

So, \(BM=QN\)   …(i)

In \(\triangle ABM\) and \(\triangle PQN\)

\(AB=PQ\)  (Given)

\(BM=QN\)   (From (i))

\(AM=PN\)  (Given)

Therefore,

\(\triangle ABM≅\triangle PQN\)  (By SSS congruence rule)

\(\angle ABM=\angle PQN\)  (By CPCT)

So, \(\angle ABC=\angle PQR\)   ..(ii)

(ii) \(\triangle ABC≅\triangle PQR\)

ANswer: In \(\triangle ABC\) and \(\triangle PQR\).

\(AB=PQ\)  (Given)

\(\angle ABC=\angle PQR\)  (from (ii))

\(BC=QR\)  (Given)

Therefore,

\(\triangle ABC≅\triangle PQR\)   (By SAS congruence rule)

Question 4: \(Be\) and \(CF\) are two equal altitudes of a triangle \(ABC\). Using \(RHS\) congruence rule, prove that the triangle \(ABC\) is isosceles.

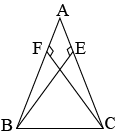
Answer: In \(\triangle BEC\) and \(\triangle CFB\),

\(\angle BEC=\angle CFB\)   (Each \(90^0\))

\(BC=CB\)  (Common)

\(Be=CF\)  (Given)

Therefore,

\(\triangle BEC≅\triangle CFB\)  (By RHS congruency)

Therefore,

\(\angle BCE=\angle CBF\)  (By CPCT)

Therefore, \(AB=AC\)  (Sides opposite to equal angles of a triangle are equal)

Hence, \(\triangle ABC\) is isosceles.

Question 5: \(ABC\) is an isosceles triangle with \(AP\bot BC\) to show that \(\angle B=\angle C\).

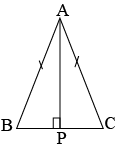
Answer: In \(\triangle APB\) and \(\triangle APC\),

\(\angle APB=\angle APC\)  (Each \(90^0\))

\(AB=AC\)  (given)

\(AP=AP\)  (Common)

Therefore,

\(\triangle APB≅\triangle APC\)  (Using RHS congruence rule)

Therefore, \(\angle B=\angle C\)   (By CPCT)